题目内容
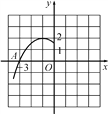
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：
①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0；⑤4ac﹣b2＜0，正确的序号是_____．
【答案】②③⑤．
【解析】令x=1，y=a+b+c>0，
故①错误；
令x=1，y=ab+c<0，
故②正确；
由于对称轴x=
<1，a<0，
∴b>2a，
∴2a+b<0，
故③正确；
由图象可知：a<0，c>0，
对称轴：x=
>0，
∴b>0
∴abc<0，
故④错误；
由于抛物线与x轴有两个交点，
∴△=b4ac>0，
即4acb<0，故⑤正确；
故答案为：②③⑤
点睛: 此题考查了二次函数图象与系数的关系，以及二次函数的性质，熟练掌握二次函数的性质是解本题的关键．
练习册系列答案
相关题目
【题目】已知函数
，画出图象并根据函数图象回答下列问题：
（1）列表、描点、连线
x | |||||
|
（2）
的两个解是多少？
（3）x取何值时，y＞0？
（4）x取何值时，抛物线在x轴上或下方？
（5）抛物线
与直线y=k有唯一的交点，则k= ．
