Question

【题目】已知函数，画出图象并根据函数图象回答下列问题：

（1）列表、描点、连线

x

（2）的两个解是多少？

（3）x取何值时，y＞0？

（4）x取何值时，抛物线在x轴上或下方？

（5）抛物线与直线y=k有唯一的交点，则k=　 　．

Answer 1

【答案】（1）答案见解析；（2）x1=2、x2=6；（3）当x＜2或x＞6时；（4）当2≤x≤6时，抛物线在x轴上或下方；（5）﹣2．

【解析】试题分析: （1）完成表格、画出函数图象，根据抛物线与x轴交点横坐标即为该方程的解即可得；

（2）根据函数图象位于x轴上方部分对应的x的范围即为y＞0的解集可得；

（3）由抛物线位于x轴上或下方部分所对应的x的范围即可得；

（4）由直线y=﹣2与抛物线有唯一交点可得答案．

试题解析:

解：（1）函数图象如下：

x	1	2	3	4	6
y=﹣4x+6		0	﹣	2	0

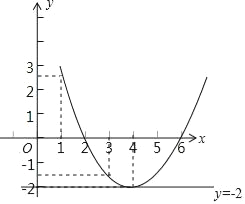
由函数图象可知， ﹣4x+6=0的两个解是x1=2、x2=6；

（2）当x＜2或x＞6时，y＞0；

（3）当2≤x≤6时，抛物线在x轴上或下方；

（4）由图可知，直线y=﹣2与抛物线只有唯一交点，

∴k=﹣2，

故答案为：﹣2．