题目内容
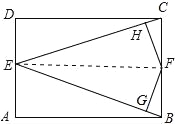
【题目】如图，在矩形ABCD中，AB=3，BC=2，点E为AD中点，点F为BC边上任一点，过点F分别作EB，EC的垂线，垂足分别为点G，H，则FG+FH为（ ）.
A．
B．
C．
D．
【答案】D．
【解析】
试题分析：先连接EF，由矩形的性质得出AB=CD=3，AD=BC=2，∠A=∠D=90°，由勾股定理求出BE，由SAS证明△ABE≌△DCE，得出BE=CE=
，再由△BCE的面积=△BEF的面积+△CEF的面积，即可得出结果．如图所示：∵四边形ABCD是矩形，∴AB=CD=3，AD=BC=2，∠A=∠D=90°，∵点E为AD中点，∴AE=DE=1，∴BE=
=
=，在△ABE和△DCE中，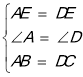
，∴△ABE≌△DCE（SAS），∴BE=CE=，∵△BCE的面积=△BEF的面积+△CEF的面积，∴
BC×AB=BE×FG+CE×FH，即BE（FG+FH）=BC×AB，即（FG+FH）=2×3，解得：FG+FH=
；故选：D．
练习册系列答案
相关题目
【题目】某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：
鸭的质量/kg | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/min | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
若鸭的质量为3.2kg时，烤制时间为_____min．
