题目内容
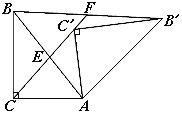
【题目】如图,Rt△ABC中,∠ACB=90°,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
(1)证明:△AC C′∽△AB B′;
(2)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时AC=BF,并说明理由.
【答案】(1)证明见解析;(2)β=2α时AC=BF.
【解析】
(1)Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,可得AC=AC′,AB=AB′,∠CA C′=∠B AB′,再根据![]() ,即可证明△AC C′∽△AB B′;(2)欲证AC=BF,需证△AEC≌△FEB,则需证BE=CE,由已知可证∠BCE=∠ABC=a,即β=2α时,△AEC≌△FEB,故得证.
,即可证明△AC C′∽△AB B′;(2)欲证AC=BF,需证△AEC≌△FEB,则需证BE=CE,由已知可证∠BCE=∠ABC=a,即β=2α时,△AEC≌△FEB,故得证.
解:(1)证明:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的
∴AC=AC′,AB=AB′,∠CA C′=∠B AB′
∴![]()
∴△AC C′∽△AB B′
(2)当β=2α时AC=BF
证明:∵AC=AC′
∴∠AC C′=∠A C′C=![]() (180°-∠C AC′)=90°-
(180°-∠C AC′)=90°-![]() β=90°-α
β=90°-α
∵∠BCE=∠ACB-∠A C C′=90°-(90°-α)=α
∴∠BCE=∠ABC
∴BE=CE
∵∠ACE=∠ABF,∠AEC=∠FEB
∴△AEC≌△FEB
∴AC=BF.

练习册系列答案
相关题目
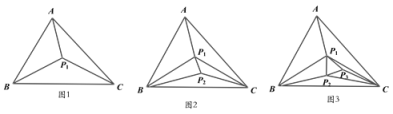
【题目】(问题背景)在△ABC内部,有地点![]() ,可构成3个不重叠的小三角形(如图1)
,可构成3个不重叠的小三角形(如图1)
(探究发现)当△ABC内的点的个数增加时,若其他条件不变,探究三角形内互不重叠的小三角形的个数情况。
(1)填表:
三角形内点的个数n | 1 | 2 | 3 | 4 | …… |
不重叠三角形个数S | …… |
(2)当△ABC内部有2019个点(![]() ,
,![]() ……
……![]() )时,三角形内不重叠的小三角形的个数S为多少?
)时,三角形内不重叠的小三角形的个数S为多少?