题目内容
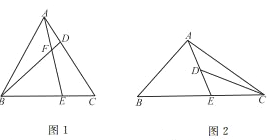
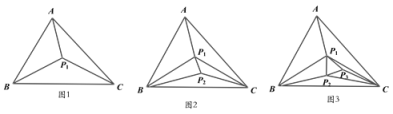
【题目】(问题背景)在△ABC内部,有地点![]() ,可构成3个不重叠的小三角形(如图1)
,可构成3个不重叠的小三角形(如图1)
(探究发现)当△ABC内的点的个数增加时,若其他条件不变,探究三角形内互不重叠的小三角形的个数情况。
(1)填表:
三角形内点的个数n | 1 | 2 | 3 | 4 | …… |
不重叠三角形个数S | …… |
(2)当△ABC内部有2019个点(![]() ,
,![]() ……
……![]() )时,三角形内不重叠的小三角形的个数S为多少?
)时,三角形内不重叠的小三角形的个数S为多少?
【答案】(1)3,5,7,9;
(2)4039.
【解析】
根据前三个探究不难发现,三角形内部每增加一个点,不重叠的小三角形的个数增加2个,根据此规律写出当△ABC内部有m个点时,三角形内不重叠的小三角形的个数为3+2(m-1),然后计算即可.
(1)当△ABC内部有1个点时,三角形内不重叠的小三角形的个数为:3=3+2(1-1),
当△ABC内部有2个点时,三角形内不重叠的小三角形的个数为:5=3+2(2-1),
当△ABC内部有3个点时,三角形内不重叠的小三角形的个数为:7=3+2(3-1),
当△ABC内部有4个点时,三角形内不重叠的小三角形的个数为:9=3+2(4-1),
…,
所以,当△ABC内部有m个点时,三角形内不重叠的小三角形的个数为:3+2(m-1).
故表中应依次填:3,5,7,9;
(2)由(1)可得:当m=2019时,3+2×(2019-1)=4039(个),
答:当△ABC内部有2019个点(P1,P2……P2019)时,三角形内不重叠的小三角形的个数S为4039.

练习册系列答案
相关题目