题目内容
在如图所示的平面直角坐标系中,点C在y轴的正半轴上,四边形OABC为平行四边形,OA=2,∠AOC=60°,以OA为直径的⊙P经过点C,交BC于点D,DE⊥AB,交AB于E.(1)求点A和B的坐标;
(2)求证:DE是⊙P的切线;
(3)小明在解答本题时,发现连结DA并延长,交x轴于点N,则△AON是等腰三角形.由此,他断定:“x轴上一定存在除点N以外的点Q,使△AOQ也是等腰三角形,且点Q一定在⊙P外”.你同意他的看法吗?请充分说明理由.
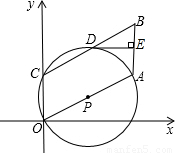
【答案】分析:(1)首先得出,∠ACO=90°,进而利用OA=2,∠AOC=60°,得出OC=1,AC=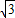 ,即可得出A点坐标,进而利用平行四边形的性质得出B点坐标;
,即可得出A点坐标,进而利用平行四边形的性质得出B点坐标;
(2)首先得出四边形OADC为等腰梯形,进而得出△PAD为等边三角形,从而得出∠BAD=∠PDA,以及PD∥AB,即可得出答案;
(3)分别根据①当OA=OQ时,②当OQ=AQ时求出Q点坐标即可.
解答:(1)解:连结AC,
∵OA为⊙P的直径,∴∠ACO=90°,
又∵OA=2,∠AOC=60°,∴OC=1,AC=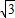 ,
,
∴A点坐标为(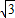 ,1),
,1),
∵OABC为平行四边形,
∴AB=OC,∴B点坐标为(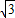 ,2).
,2).
(2)证明:连结PD、AD,
∵四边形OABC是平行四边形,
∴CD∥OA,
∴弧OC=弧AD,∴OC=AD,
∴四边形OADC为等腰梯形,
∴∠DAO=∠AOC=60°,
∵PA=PD,
∴△PAD为等边三角形,
∴∠PDA=60°,
∵∠BAO=180°-60°=120°,∠DAO=60°,
∴∠BAD=60°,
∴∠BAD=∠PDA,∴PD∥AB,
∵DE⊥AB,
∴DE⊥PD,
∴DE是⊙P的切线.
(3)解:不同意.
理由如下:
①当OA=OQ时,
以点O为圆心,OA为半径画弧交x轴于Q1和Q3两点,
得点Q1(-2,0),Q3(2,0)
②当OQ=AQ时,作OA的中垂线,交x轴于点Q2,
OQ2= <
<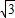 ,点Q2(
,点Q2(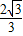 ,0).
,0).
因此,在x轴上,除了N点外,既存在⊙P内的点Q2,
又存在⊙P外的点Q1、Q3,它们分别使△AOQ为等腰三角形.
点评:此题主要考查了等腰三角形的性质以及切线的判定和锐角三角函数关系等知识,注意分类讨论思想的应用不要漏解.
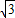 ,即可得出A点坐标,进而利用平行四边形的性质得出B点坐标;
,即可得出A点坐标,进而利用平行四边形的性质得出B点坐标;(2)首先得出四边形OADC为等腰梯形,进而得出△PAD为等边三角形,从而得出∠BAD=∠PDA,以及PD∥AB,即可得出答案;
(3)分别根据①当OA=OQ时,②当OQ=AQ时求出Q点坐标即可.
解答:(1)解:连结AC,
∵OA为⊙P的直径,∴∠ACO=90°,
又∵OA=2,∠AOC=60°,∴OC=1,AC=
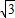 ,
,∴A点坐标为(
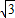 ,1),
,1),∵OABC为平行四边形,
∴AB=OC,∴B点坐标为(
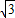 ,2).
,2).(2)证明:连结PD、AD,
∵四边形OABC是平行四边形,
∴CD∥OA,
∴弧OC=弧AD,∴OC=AD,
∴四边形OADC为等腰梯形,

∴∠DAO=∠AOC=60°,
∵PA=PD,
∴△PAD为等边三角形,
∴∠PDA=60°,
∵∠BAO=180°-60°=120°,∠DAO=60°,
∴∠BAD=60°,
∴∠BAD=∠PDA,∴PD∥AB,
∵DE⊥AB,
∴DE⊥PD,
∴DE是⊙P的切线.
(3)解:不同意.
理由如下:
①当OA=OQ时,
以点O为圆心,OA为半径画弧交x轴于Q1和Q3两点,
得点Q1(-2,0),Q3(2,0)
②当OQ=AQ时,作OA的中垂线,交x轴于点Q2,
OQ2=
 <
<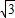 ,点Q2(
,点Q2(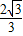 ,0).
,0).因此,在x轴上,除了N点外,既存在⊙P内的点Q2,
又存在⊙P外的点Q1、Q3,它们分别使△AOQ为等腰三角形.
点评:此题主要考查了等腰三角形的性质以及切线的判定和锐角三角函数关系等知识,注意分类讨论思想的应用不要漏解.

练习册系列答案
相关题目

 22、(1)在如图所示的平面直角坐标系中,先画出△OAB关于y轴对称的图形,再画出△OAB绕点O旋转180°后得到的图形.
22、(1)在如图所示的平面直角坐标系中,先画出△OAB关于y轴对称的图形,再画出△OAB绕点O旋转180°后得到的图形.
 20、在如图所示的平面直角坐标系中,描出点A(-2,1),B(3,1),C(-2,-2),D(3,-2)四个点.
20、在如图所示的平面直角坐标系中,描出点A(-2,1),B(3,1),C(-2,-2),D(3,-2)四个点. 11、△ABC在如图所示的平面直角坐标系中.
11、△ABC在如图所示的平面直角坐标系中. Rt△ABC在如图所示的平面直角坐标系中.
Rt△ABC在如图所示的平面直角坐标系中.