题目内容
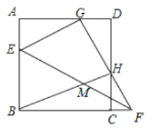
【题目】如图,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'CD',B'C与AD交于点E,AD的延长线与A′D′交于点F.
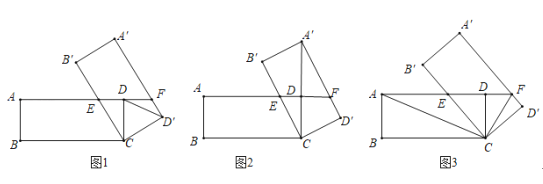
(1)如图1,当a=60°时,连接DD',求DD'和A'F的长;
(2)如图2,当矩形A′B′CD′的顶点A'落在CD的延长线上时,求EF的长;
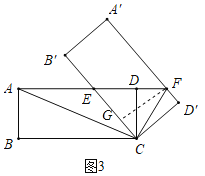
(3)如图3,当AE=EF时,连接AC,CF,求证:∠ACF=90°.
【答案】(1)DD'=3;A'F= 4-![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)由旋转的性质可得CD=CD'=3,A'D'=AD=4,∠DCD'=60°,∠ADC=∠A'D'C=90°,由“HL”可证Rt△CDF≌Rt△CD'F,可得∠DCF=∠D'CF=30°,由锐角三角函数可求DF的长,即可求A'F的长;
(2)由勾股定理可求A'C=5,可得A'D=2,通过证明△ECD∽△A'CB',可得![]() ,可求DE的长,由平行线分线段成比例可得
,可求DE的长,由平行线分线段成比例可得![]() ,可求DF的长,即可求EF的长;
,可求DF的长,即可求EF的长;
(3)如图3,过点F作FG⊥B'C于G,由面积法可证EF=EC=AE,由直角三角形的判定可得∠ACF=90°.
(1)∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=4,
∵将矩形ABCD绕点C按顺时针方向旋转60°角,
∴CD=CD'=3,A'D'=AD=4,∠DCD'=60°,∠ADC=∠A'D'C=90°,
∴△DCD'是等边三角形,
∴DD'=CD=3,∠CDD'=∠CD'D=60°,
∴∠FDD'=∠FD'D=30°,
如图1,连接CF,
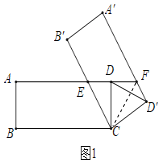
∵CD=CD',CF=CF,
∴Rt△CDF≌Rt△CD'F(HL)
∴∠DCF=∠D'CF=30°
∵tan∠DCF=![]() ,
,
∴DF=3×![]() ,
,
∴D'F=![]() ,
,
∴A'F=A'D'-D'F=4-![]() ,
,
(2)在Rt△A'B'C中,![]() ,
,
∵CD=3,
∴A'D=A'C-CD=2,
∵∠DCE=∠A'CB',∠CDE=∠B'=90°,
∴△ECD∽△A'CB',
∴![]()
∴![]()
∴DE=![]()
∵A'D'∥B'C
∴![]()
∴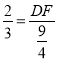
∴DF=![]()
∴EF=DE+DF=![]()
(3)如图3,过点F作FG⊥B'C于G,
∴FG=CD'=3=CD,
∵S△CEF=![]() ×EF×CD=
×EF×CD=![]() ×EC×GF,
×EC×GF,
∴EF=EC
∵AE=EF,
∴AE=EF=EC,
∴△ACF是直角三角形,
∴∠ACF=90°

【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
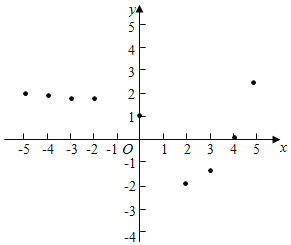
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .