题目内容
【题目】如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E,与⊙O相交于点F,连接BF.
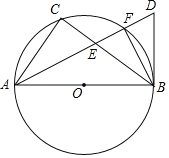
(1)求证:BD=BE;
(2)若DE=2,BD=2![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2)AE=18.
【解析】
(1)利用圆周角定理得到∠ACB=90°,再根据切线的性质得∠ABD=90°,则∠BAD+∠D=90°,然后利用等量代换证明∠BED=∠D,从而判断BD=BE;
(2)利用圆周角定理得到∠AFB=90°,则根据等腰三角形的性质DF=EF=![]() DE=1,再证明△DFB∽△DBA,利用相似比求出AD的长,然后计算AD-DE即可.
DE=1,再证明△DFB∽△DBA,利用相似比求出AD的长,然后计算AD-DE即可.
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAE+∠CEA=90°,
而∠BED=∠CEA,
∴∠CAE+∠BED=90°,
∵BD是⊙O的切线,
∴BD⊥AB,
∴∠ABD=90°,
∴∠BAD+∠D=90°,
又∵AF平分∠CAB,
∴∠CAE=∠BAD,
∴∠BED=∠D,
∴BD=BE;
(2)解:∵AB为直径,
∴∠AFB=90°,且BE=BD,
∴DF=EF=![]() DE=1,
DE=1,
∵∠FDB=∠BDA,
∴△DFB∽△DBA,
∴![]() =
=![]() ,
,
∴DA=2![]() ×2
×2![]() =20,
=20,
∴AE=AD﹣DE=20﹣2=18.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
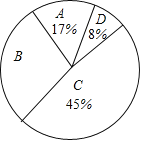
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。