题目内容
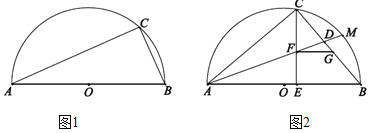
【题目】已知AB是半圆O的直径,点C在半圆O上.
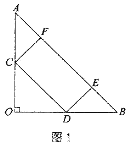
(1)如图1,若AC=3,∠CAB=30°,求半圆O的半径;
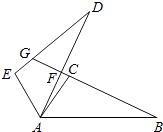
(2)如图2,M是![]() 的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
【答案】(1)半圆O的半径为![]() ;
;
(2)⊙D与直线AC相切,理由见解析
【解析】试题分析:(1)依据直径所对的圆周角是直角可得∠C=90°,2再依据三角函数即可求解;(2) 依据△ACE与△CEB相似证出∠AEC=∠CEB=90°, 再依据M是![]() 的中点,证明CF=CD, 过点F作FP∥GB交于AB于点P, 证出△ACF≌△APF,得出CF=FP,再证四边形FPBG是平行四边形,得到 FP=GB从而CD=GB,点D到直线AC的距离为线段CD的长.
的中点,证明CF=CD, 过点F作FP∥GB交于AB于点P, 证出△ACF≌△APF,得出CF=FP,再证四边形FPBG是平行四边形,得到 FP=GB从而CD=GB,点D到直线AC的距离为线段CD的长.
试题解析:
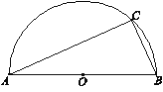
(1)∵ AB是半圆O的直径,
∴ ∠C=90°.
在Rt△ACB中,AB=![]()
=![]()
=2![]() .
.
∴ OA=![]()
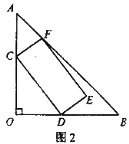
(2)
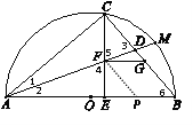
⊙D与直线AC相切.
理由如下:
由(1)得∠ACB=90°.
∵ ∠AEC=∠ECB+∠6,
∴ ∠AEC>∠ECB,∠AEC>∠6.
∵ △ACE与△CEB相似,
∴ ∠AEC=∠CEB=90°.
在Rt△ACD,Rt△AEF中分别有
∠1+∠3=90°,∠2+∠4=90°.
∵ M是![]() 的中点,
的中点,
∴ ∠COM=∠BOM.
∴ ∠1=∠2,
∴ ∠3=∠4.
∵ ∠4=∠5,
∴ ∠3=∠5.
∴ CF=CD.
过点F作FP∥GB交于AB于点P,则∠FPE=∠6.
在Rt△AEC,Rt△ACB中分别有
∠CAE+∠ACE=90°,∠CAE+∠6=90°.
∴ ∠ACE=∠6=∠FPE.
又∵ ∠1=∠2,AF=AF,
∴ △ACF≌△APF.
∴ CF=FP.
∵ FP∥GB,FG∥AB,
∴ 四边形FPBG是平行四边形.
∴ FP=GB.
∴ CD=GB.
∵ CD⊥AC,
∴ 点D到直线AC
∴ ⊙D与直线AC相切.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】有这样一个问题:探究函数y=![]() 的图象与性质。小慧根据学习函数的经验,对函数y=
的图象与性质。小慧根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;
(2)列出y与x的几组对应值。请直接写出m的值,m=________;
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
①_____________________________________________;
②____________________________________________。