题目内容
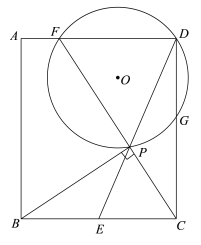
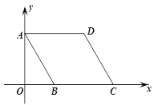
【题目】如图,单位长度为![]() 的网格坐标系中,一次函数
的网格坐标系中,一次函数![]() 与坐标轴交于
与坐标轴交于![]() 、
、![]() 两点,反比例函数
两点,反比例函数![]()
![]() 经过一次函数上一点
经过一次函数上一点![]() .
.
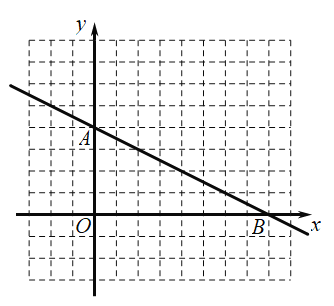
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于
交于![]() 、
、![]() 两点,在图中用直尺与
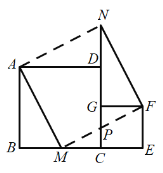
两点,在图中用直尺与![]() 铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
①四个顶点均在格点上,且其中两个顶点分别是点![]() 、点
、点![]() ;
;
②矩形的面积等于![]() 的值.
的值.
【答案】(1)![]() ,图形见解析;(2)
,图形见解析;(2)![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】
(1)由图可知A、B两点坐标,于是可以求出一次函数的解析式,反比例函经过一次函数上一点C,所以可以通过一次函数解析式求出C点坐标,既而求出反比例函数的解析式;明确反比例函数的解析式即可画出反比例函数图像.
(2)由图可知,一次函数与反比例函数相交于B、C两点,所以根据图像,当![]() 时,一次函数的y值大于反比例函数的y值.
时,一次函数的y值大于反比例函数的y值.
(3)根据题意,首先满足矩形的四个顶点均在格点上,其次,满足矩形的面积为10,先明确![]() 的值,然后要分两种情况讨论,分别是以
的值,然后要分两种情况讨论,分别是以![]() 为边和以
为边和以![]() 为对角线去思考画图即可.
为对角线去思考画图即可.
解(1)由图知点A坐标为(0,4),点B的坐标为(8,0),
一次函数![]() 经过A、B两点,∴
经过A、B两点,∴![]() ,
,
解得: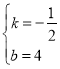 ,
,
∴一次函数解析式为:![]() ,
,
∵![]() 经过点C (2,a),
经过点C (2,a),
∴a=-1+4=3,
∴点C坐标为(2,3),
∵反比例函数![]() 经过点C(2,3),
经过点C(2,3),
∴![]() ,
,
∴反比例函数解析式为:![]() ;
;
当x=6时,y=1,所以反比例函数过D(6,1)
描绘出反比例函数![]() (x>0)的图像如下图:
(x>0)的图像如下图:
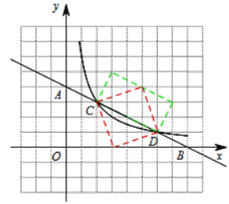
(2)由图可知,一次函数与反比例函数交于C、D两点,通过(1)得到C、D两点坐标,根据图中反比例函数与一次函数的位置关系,当![]() 时满足
时满足![]() .
.
故![]()
(3)画出两个以C、D为顶点的矩形如上图所示,理由如下:
由图像可知点C(2,3),点D(6,1),
依据勾股定理可得CD=![]() =
=![]() ,已知矩形面积为10的情况下,分类讨论:
,已知矩形面积为10的情况下,分类讨论:
若以CD为边构造矩形,则矩形的另一边为![]() ;
;
若以CD为对角线的情况下构造矩形,此时矩形为正方形,得其边长为![]() .
.
故构造符合题意的矩形共有3个.

 备战中考寒假系列答案
备战中考寒假系列答案