题目内容
已知⊙O中，
=
．
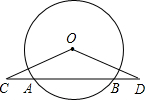
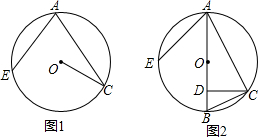
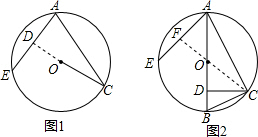
（1）如图1，求证：CO⊥AE；
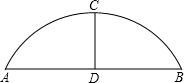
（2）如图2，CD⊥直径AB于D，若BD=1，AE=4，求⊙O的半径．
 |
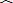| AC |
|
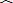| CE |
（1）如图1，求证：CO⊥AE；
（2）如图2，CD⊥直径AB于D，若BD=1，AE=4，求⊙O的半径．
（1）证明：延长CO交AE于点D，
∵
=
，CD过圆心，
∴CO⊥AE；
（2）设⊙O的半径为r，连接CO并延长交AE于点F，
∵
=
，CD过圆心，AE=4，
∴OF⊥AE，
∴AF=
AE=
×4=2，
∵CD⊥AB，∠AOF=∠COD，
∴在△OAF与△OCD中，
∵
，
∴△OAF≌△OCD，
∴OF=OD=r-1，
∴在Rt△AOF中，OA2=AF2+OF2，即r2=22+（r-1）2，解得r=
．
∵
|
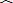| AC |
|
| CE |
∴CO⊥AE；
（2）设⊙O的半径为r，连接CO并延长交AE于点F，
∵
|
| AC |
|
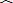| CE |
∴OF⊥AE，
∴AF=
| 1 |
| 2 |
| 1 |
| 2 |
∵CD⊥AB，∠AOF=∠COD，
∴在△OAF与△OCD中，
∵
|
∴△OAF≌△OCD，
∴OF=OD=r-1，
∴在Rt△AOF中，OA2=AF2+OF2，即r2=22+（r-1）2，解得r=
| 5 |
| 2 |
练习册系列答案
阶梯计算系列答案
相关题目
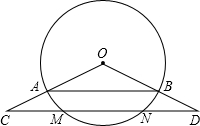，并与弧AB相交于点M、N．
