题目内容
【题目】已知关于x,y的二元一次方程ax+b=y(a,b为常数且a≠0)
(1)该方程的解有 组;若a=﹣2,b=6,且x,y为非负整数,请直接写出该方程的解;
(2)若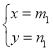 和
和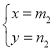 是该方程的两组解,且m1>m2
是该方程的两组解,且m1>m2
①若n1﹣n2=2(m2﹣m1),求a的值;
②若m1+m2=3b,n1+n2=ab+4,且b>2,请比较n1和n2大小,并说明理由.
【答案】(1)该方程的解有 无数 组;![]() ,
,![]() ,
,![]() ,
,![]() ,(2)①a=﹣2;②n1<n2.理由见解析.
,(2)①a=﹣2;②n1<n2.理由见解析.
【解析】
(1)a,b 值不确定,该方程有无数组解,将a=﹣2,b=6代入方程中,结合条件x,y为非负整数,即可求解.
(2)①将两组解代入方程可得式子n1=am1+b,n2=am2+b,两式相减,结合条件即可求出a的值.
②将两组解代入方程可得式子n1=am1+b,n2=am2+b,将两式化为n1+n2=a(m1+m2)+2b,将m1+m2=3b,n1+n2=ab+4代入可得ab+4=3ab+2b结合已知条件即可求解.
(1)该方程的解有 无数 组; 将a=﹣2,b=6,代入ax+b=y(a,b为常数且a≠0)
-2x+6=y,解得: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)①将两组解代入方程可得式子n1=am1+b,n2=am2+b
两式相减则可得:n1﹣n2=a(m2﹣m1),即a=﹣2;
②∵n1=am1+b,n2=am2+b,
∴n1+n2=a(m1+m2)+2b,
∴ab+4=3ab+2b,
∴ab+b=2,
∴a=![]() ,
,
∵b>2,
∴0<![]() <1,
<1,
∴﹣1<![]() <0,
<0,
∴﹣1<a<0.
又∵n1﹣n2=a(m1﹣m2),m1>m2,
∴n1﹣n2<0,
∴n1<n2.

【题目】某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?