ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌ ЫФБпаЮOABCЮЊжБНЧЬнаЮЃЌAЃЈ4ЃЌ0ЃЉЃЌBЃЈ3ЃЌ4ЃЉЃЌCЃЈ0ЃЌ4ЃЉЃЎ Еу![]() Дг
Дг![]() ГіЗЂвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ
ГіЗЂвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ![]() дЫЖЏЃЛЕу
дЫЖЏЃЛЕу![]() Дг
Дг![]() ЭЌЪБГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ
ЭЌЪБГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ![]() дЫЖЏЃЎЦфжавЛИіЖЏЕуЕНДяжеЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏЃЎЙ§Еу
дЫЖЏЃЎЦфжавЛИіЖЏЕуЕНДяжеЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏЃЎЙ§Еу![]() зї
зї![]() ДЙжБ
ДЙжБ![]() жсгкЕу
жсгкЕу![]() ЃЌСЌНсACНЛNPгкQЃЌСЌНсMQЃЎ
ЃЌСЌНсACНЛNPгкQЃЌСЌНсMQЃЎ
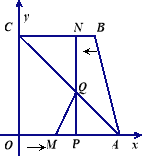
ЁО1ЁПЕу ЃЈЬюMЛђNЃЉФмЕНДяжеЕуЃЛ
ЁО1ЁПЧѓЁїAQMЕФУцЛ§SгыдЫЖЏЪБМфtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЌЕБtЮЊКЮжЕЪБЃЌSЕФжЕзюДѓЃЛ
ЁО1ЁПЪЧЗёДцдкЕуMЃЌЪЙЕУЁїAQMЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЌШєВЛДцдкЃЌ
![]() ЫЕУїРэгЩЃЎ
ЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЁО1ЁПЕуM
ЁО1ЁПОЙ§tУыЪБЃЌ![]() ЃЌ
ЃЌ ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]()
Ёп![]() =
=![]() =
=![]() ЃЌЁр
ЃЌЁр![]() Ёр
Ёр![]()
Ёр![]()
![]()
Ёр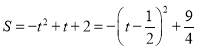 Ёп
Ёп![]() ЁрЕБ
ЁрЕБ![]() ЪБЃЌSЕФжЕзюДѓЃЎ
ЪБЃЌSЕФжЕзюДѓЃЎ
ЁО1ЁПДцдкЁЃ
ЩшОЙ§tУыЪБЃЌNB=tЃЌOM=2t ЃЌдђ![]() ЃЌ
ЃЌ![]() Ёр
Ёр![]() =
=![]() =
=![]()
ЂйШє![]() ЃЌдђ
ЃЌдђ![]() ЪЧЕШбќRtЁї
ЪЧЕШбќRtЁї![]() ЕзБп
ЕзБп![]() ЩЯЕФИпЃЌ
ЩЯЕФИпЃЌ
Ёр![]() ЪЧЕзБп
ЪЧЕзБп![]() ЕФжаЯп Ёр
ЕФжаЯп Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ ЁрЕу
ЃЌ ЁрЕу![]() ЕФзјБъЮЊЃЈ1ЃЌ0ЃЉ
ЕФзјБъЮЊЃЈ1ЃЌ0ЃЉ
ЂкШє![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() гы
гы![]() жиКЯЃЌЁр
жиКЯЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЁрЕу
ЁрЕу![]() ЕФзјБъЮЊЃЈ2ЃЌ0ЃЉ
ЕФзјБъЮЊЃЈ2ЃЌ0ЃЉ
ЁОНтЮіЁП
ЁО1ЁПгЩгкЕуMБШЕуNЯШГіЗЂВЂЧвЕуMЕФЫйЖШБШЕуNДѓЃЌПЩжЊЕуMФмЕНДяжеЕуЃЎ
ЁО1ЁПОЙ§tУыЪБПЩЕУNB=yЃЌOM-2tЃЎИљОнЁЯBCA=ЁЯMAQ=45ЁуЭЦГіQN=CNЃЌPQЕФжЕЃЎЧѓГіSгыtЕФКЏЪ§ЙиЯЕЪНКѓИљОнtЕФжЕЧѓГіSЕФзюДѓжЕЃЎ
ЁО1ЁПБОЬтЗжСНжжЧщПіЬжТлЃЈШєЁЯAQM=90ЁуЃЌPQЪЧЕШбќRtЁїMQAЕзБпMAЩЯЕФИпЃЛ
ШєЁЯQMA=90ЁуЃЌQMгыQPжиКЯЃЉЧѓГіtжЕЃЎ