Question

【题目】如图，正比例函数的图象与反比例函数的图象交于A、B两点，过点A作AC垂直x轴于点C，连结BC．若△ABC的面积为2．

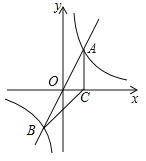
（1）求k的值；

（2）x轴上是否存在一点D，使△ABD为直角三角形？若存在，求出点D的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）k=2；（2）D（5，0）或（﹣5，0）或（，0）或D（，0）．

【解析】试题分析：（1）首先根据反比例函数与正比例函数的图象特征，可知A、B两点关于原点对称，则O为线段AB的中点，故△BOC的面积等于△AOC的面积，都等于1，然后由反比例函数的比例系数k的几何意义，可知△AOC的面积等于，从而求出k的值；

（2）先将与联立成方程组，求出A、B两点的坐标，然后分三种情况讨论：①当AD⊥AB时，求出直线AD的关系式，令y=0，即可确定D点的坐标；②当BD⊥AB时，求出直线BD的关系式，令y=0，即可确定D点的坐标；③当AD⊥BD时，由O为线段AB的中点，可得OD=AB=OA，然后利用勾股定理求出OA的值，即可求出D点的坐标．

试题解析：（1）∵反比例函数与正比例函数的图象相交于A、B两点，∴A、B两点关于原点对称，∴OA=OB，∴△BOC的面积=△AOC的面积=2÷2=1，又∵A是反比例函数图象上的点，且AC⊥x轴于点C，∴△AOC的面积=，∴，∵k＞0，∴k=2．故这个反比例函数的解析式为；

（2）x轴上存在一点D，使△ABD为直角三角形．将与联立成方程组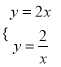得： ，解得： ， ，∴A（1，2），B（﹣1，﹣2），

①当AD⊥AB时，如图1，

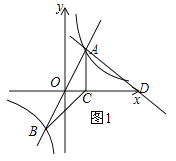
设直线AD的关系式为，将A（1，2）代入上式得： ，∴直线AD的关系式为，令y=0得：x=5，∴D（5，0）；

②当BD⊥AB时，如图2，

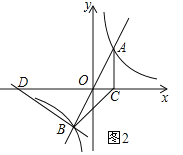
设直线BD的关系式为，将B（﹣1，﹣2）代入上式得： ，∴直线AD的关系式为，令y=0得：x=﹣5，∴D（﹣5，0）；

③当AD⊥BD时，如图3，

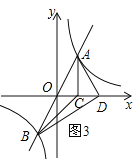
∵O为线段AB的中点，∴OD=AB=OA，∵A（1，2），∴OC=1，AC=2，由勾股定理得：OA==，∴OD=，∴D（，0），

根据对称性，当D为直角顶点，且D在x轴负半轴时，D（，0）；

故x轴上存在一点D，使△ABD为直角三角形，点D的坐标为（5，0）或（﹣5，0）或（，0）或D（，0）．