Question

如图，⊙O是O为圆心，半径为

5

的圆，直线y=kx+b交坐标轴于A、B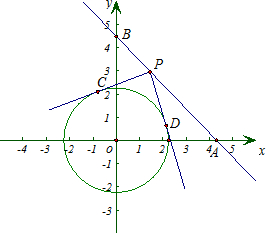两点．
（1）若OA=OB
①求k；
②若b=4，点P为直线AB上一点，过P点作⊙O的两条切线，切点分别为C、D，若∠CPD=90°，求点P的坐标；
（2）若k=-

1

2

，且直线y=kx+b分⊙O的圆周为1：2两部分，求b．

Answer 1

（1）①由OA=OB，设A点坐标（a，0），则点B的坐标（0，a），
把这两点代入直线的解析式y=kx+b得：

ak+b=0 b=a

，
解得：k=-1．
②由题意得，Rt△POC≌Rt△POD，
∴∠CPO=∠DPO=

1

2

∠CPD=45°，OP=

2

OC=

2

R=

10

，
又∵直线的函数解析式y=-x+4，
故设P点坐标（x，-x+4）
OP=

x2+(-x+4)2

=

10

，解得：x=1或3
∴P（1，3）或（3，1）
（2）由题意得，当直线被切割的弦所对的圆周角为120°时，
弦长为2Rsin60°=

3

R时，弦分圆周为1：2，符合题意，
联立直线和圆的方程得，

y=- 1 2 x+b① x2+y2=5②

将①代入②消去y得x²+（-

1

2

x+b）²=5，即

5

4

x²-bx+b²-5=0
利用根与系数的关系可得（x₁-x₂）²=（x₁+x₂）²-4x₁x₂=

16

25

b²-

16

5

b²+16=-

64

25

b²+16，
将①代入②消去x得（2b-2y）²+y²=5，即5y²-8by+4b²-5=0
利用根与系数的关系可得（y₁-y₂）²=（y₁+y₂）²-4y₁y₂=

16

25

b²-

16

5

b²+16=-

64

25

b²+16，
将解得的两交点坐标用两点间距离公式得

(x1-x2)2+(y1-y2)2

=

3

R
解得：b=±

5

4

．