题目内容
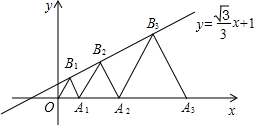
如图,已知:点A1、A2、A3、…在平面直角坐标系x轴上,点B1、B2、B3、…在直线y=
x+1上,△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,求A2013的横坐标______.
| ||
| 3 |

设直线y=
x+1分别于x轴、y轴于点C、D,
∴点C(-
,0),点D(0,1),
∴OC=
,OD=1,
∴tan∠OCD=
=
,
∴∠OCD=30°,
∵△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,
∴∠A1OB1=∠A2A1B2=∠A3A2B3=60°,
∴∠OB1C=∠A1B2C=∠A2B3C=∠OCD=30°,
∴OB1=OC=
,A1B2=A1C,A2B3=A2C,
∴OA1=OB1=
,OA2=OA1+A1A2=OA1+A1B1=
+2
=3
,
同理:OA3=7
,OA4=15
,
∴OAn=(2n-1)
.
∴OA2013=(22013-1)
.
故答案为:(22013-1)
.

| ||
| 3 |
∴点C(-
| 3 |
∴OC=
| 3 |
∴tan∠OCD=
| 1 | ||
|
| ||
| 3 |
∴∠OCD=30°,
∵△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,
∴∠A1OB1=∠A2A1B2=∠A3A2B3=60°,
∴∠OB1C=∠A1B2C=∠A2B3C=∠OCD=30°,
∴OB1=OC=
| 3 |
∴OA1=OB1=
| 3 |
| 3 |
| 3 |
| 3 |
同理:OA3=7
| 3 |
| 3 |
∴OAn=(2n-1)
| 3 |
∴OA2013=(22013-1)
| 3 |
故答案为:(22013-1)
| 3 |


练习册系列答案
相关题目
 A向点A匀速运动;设点P、Q运动时间为t(秒)
A向点A匀速运动;设点P、Q运动时间为t(秒) y(元)是用水量x(吨)的函数,其函数图象如图所示.
y(元)是用水量x(吨)的函数,其函数图象如图所示.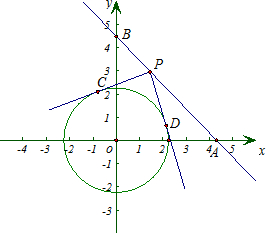 两点.
两点.

 之间关系如图.
之间关系如图.


