题目内容
甲、乙两人分别以骑摩托车和步行的方式从A地前往B地．甲骑车的速度为30千米/小时，甲到达B地立即返回．乙步行的速度为15千米/小时．已知A，B两地的距离为60千米，甲、乙行驶过程中与A地的距离y（千米）关于时间x（小时）的函数图象如图所示．
（1）求甲在行驶的整个过程中，y与x之间的函数关系式；
（2）甲、乙两人同时出发后，经过多长时间相遇？
（1）求甲在行驶的整个过程中，y与x之间的函数关系式；
（2）甲、乙两人同时出发后，经过多长时间相遇？
（1）∵甲的速度是30千米/小时，而全程是60千米，
∴甲走完全程用的时间是60÷30=2小时，甲往返用的时间是120÷30=4小时．
∴A（2，60），B（4，0）．
∵乙的速度是15千米/小时，
∴乙走完全程需要的时间是60÷15=4小时．
∴C（4，60）．
当0≤x≤2时，设y与x之间的函数关系式为y1=k1x，由题意，得
60=2k1，
∴k1=30，
∴y1=30x；
当2＜x≤4时，设y与x之间的函数关系式为y2=k2x+b，由题意，得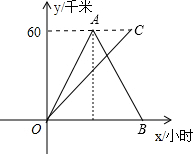
，
解得：
，
∴y2=-30x+120
∴y=
（2）设OC的解析式为y3=k3x，由题意，得
60=4k，
k=15，
∴y3=15x（0≤x≤4），
当y2=y3时，
-30x+120=15x，
x=
，
∴甲、乙两人同时出发后，经过
小时相遇．
∴甲走完全程用的时间是60÷30=2小时，甲往返用的时间是120÷30=4小时．
∴A（2，60），B（4，0）．
∵乙的速度是15千米/小时，
∴乙走完全程需要的时间是60÷15=4小时．
∴C（4，60）．
当0≤x≤2时，设y与x之间的函数关系式为y1=k1x，由题意，得
60=2k1，
∴k1=30，
∴y1=30x；
当2＜x≤4时，设y与x之间的函数关系式为y2=k2x+b，由题意，得
|
解得：
|
∴y2=-30x+120
∴y=
|
（2）设OC的解析式为y3=k3x，由题意，得
60=4k，
k=15，
∴y3=15x（0≤x≤4），
当y2=y3时，
-30x+120=15x，
x=
| 8 |
| 3 |
∴甲、乙两人同时出发后，经过
| 8 |
| 3 |
练习册系列答案
相关题目
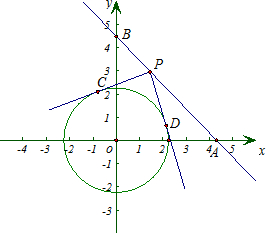两点．
以每秒2个单位的速度移动，同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动．设移动的时间为t秒．
之间关系如图．
极性．工人每天加工零件获得的加工费y（元）与加工个数x（个）之间的函数图象为折线OA-AB-BC，如图所示．
