题目内容
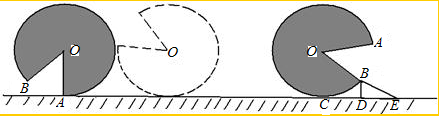
如图，水平地面上有一面积为
πcm2的扇形AOB，半径OA=3cm，且OA与地面垂直．在没有滑动的情况下，将扇形向右滚动至与三角块BDE接触为止，此时，扇形与地面的接触点为C，已知∠BCD=30°，则O点移动的距离为（ ）
| 15 |
| 2 |
| A、3πcm | ||
| B、4πcm | ||
C、
| ||
| D、5πcm |
分析：点O移动的距离即为优弧AB的长度再减去弧BC的长度即可．根据扇形的面积求出圆心角，连接OC、BC，可求得△OBC为等边三角形，从而得出答案．
解答：解：∵扇形AOB的面积为
πcm2，
∴圆心角=
=300°，
连接OC、BC，
∵∠BCD=30°，
∴∠BOC=60°，
∴优弧AC=
=4πcm．
故选B．
| 15 |
| 2 |
∴圆心角=
| 360×15π |
| 2×9π |
连接OC、BC，
∵∠BCD=30°，
∴∠BOC=60°，
∴优弧AC=
| 240×π×3 |
| 180 |
故选B．
点评：本题考查了扇形的有关计算，要熟练掌握弧长公式和扇形的面积公式：l=
，S=
．
| nπr |
| 180 |
| nπr2 |
| 360 |
练习册系列答案
阅读快车系列答案
相关题目
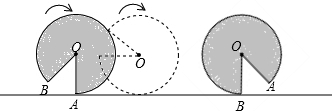
如图，水平地面上有一半径为6cm、面积为30πcm2的扇形，且OA与地面垂直．在没有滑动的情况下，将扇形向右滚动至OB与地面垂直的位置为止，则点O移动的距离为
如图，水平地面上有一长、宽分别为4cm、3cm的长方形木块，先绕点D向右依次无滑动地翻转或平移，使其一边紧贴墙壁MN，若A点开始距MN12cm，则在翻转或平移的过程中，A点所经过的路径长为