题目内容
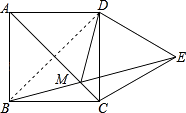
【题目】如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( ) 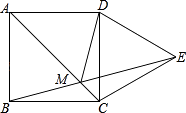
A.75°
B.60°
C.54°
D.67.5°
【答案】B
【解析】
解答:解:如图,连接BD,
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,BC=EC,
∴∠EBC=∠BEC= ![]() (180°-∠BCE)=15°
(180°-∠BCE)=15°
∵∠BCM= ![]() ∠BCD=45°,
∠BCD=45°,
∴∠BMC=180°-(∠BCM+∠EBC)=120°,
∴∠AMB=180°-∠BMC=60°
∵AC是线段BD的垂直平分线,M在AC上,
∴∠AMD=∠AMB=60°
故选B
分析:连接BD,根据BD,AC为正方形的两条对角线可知AC为BD的垂直平分线,所以∠AMD=AMB,要求∠AMD,求∠AMB即可.本题考查的正方形的对角垂直平分的性质,根据垂直平分线的性质可以求得∠AMD=∠AMB,确定AC和BD垂直平分是解题的关键

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目