题目内容
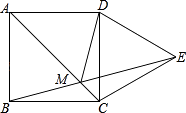
【题目】搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2 , 则被分隔开的△CON的面积为( ) 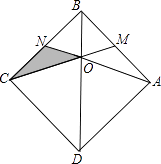
A.96cm2
B.48cm2
C.24cm2
D.以上都不对
【答案】B
【解析】
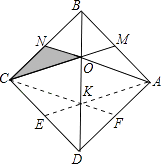
解答:解:找到CD的中点E,找到AD的中点F,连接CF,AE,
则CM∥EA,AN∥FC,△BOM∽△BKA,
∴ ![]() =
= ![]() =
= ![]() ,
,
同理可证: ![]() =
= ![]() =
= ![]() ,
,
故DK=KO=OB,
∴△BOC和△BOA的面积和为 ![]() 正方形ABCD的面积,
正方形ABCD的面积,
∵CN=NB=AM=BM,
∴△OCN的面积为 ![]() △BOC和△BOA的面积和,
△BOC和△BOA的面积和,
∴△OCN的面积为 ![]() =48cm2,
=48cm2,
故选B
分析:先证明BO为正方形ABCD的对角线BD的 ![]() ,再求证△CNO,△NBO,△AMO,△BMO的面积相等,即△CON的面积为正方形面积的
,再求证△CNO,△NBO,△AMO,△BMO的面积相等,即△CON的面积为正方形面积的 ![]() .本题考查了正方形内中位线的应用,考查了正方形四边均相等的性质,解本题的关键是求证BO=
.本题考查了正方形内中位线的应用,考查了正方形四边均相等的性质,解本题的关键是求证BO= ![]() BD,△OCN的面积为
BD,△OCN的面积为 ![]() △BOC和△BOA的面积和
△BOC和△BOA的面积和

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目