题目内容
【题目】如图,将一块三角板ABC的直角顶点C放在直尺的一边PQ上,直尺的另一边MN与三角板的两边AC、BC分别交于两点E、D,且AD为∠BAC的平分线,∠B=300 , ∠ADE=150.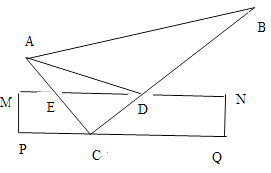
(1)求∠BDN的度数;
(2)求证:CD=CE.
【答案】
(1)解:在直角三角形ABC中,∠ACB=900 , ∠B=300,
∴∠BAC=600,又AD平分∠BAC,
∴∠CAD=300,又∠ACD=900,
∴∠CDA=600
又∠ADE=150 ,
∴∠CDE=∠CDA-∠ADE=600-150=450
∴∠BDN=∠CDE=450
(2)解:在△CED中,∠ECD=900 , ∠CDE=450
∴∠CED=450
∴ CD=CE
【解析】(1)∠BDN可转化为∠CDE,∠CDE再转化为∠CDA-∠ADE=600-150=450;(2)利用(1)的结论,∠CDE=450 , ∠ECD=900,可得出,CED=450
进而证得CD=CE.
【考点精析】本题主要考查了三角形的内角和外角和等腰三角形的判定的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目