题目内容
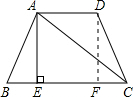
如图，在等腰梯形ABCD中，已知AD∥BC，AB=CD，AE⊥BC于E，∠B=60°，∠DAC=45°，AC=
，求梯形ABCD的周长？
| 6 |
∵AD∥BC，∠DAC=45°，
∴∠ACB=45°
∵AE⊥BC，AC=
，
∴AE=EC=
，
∵∠B=60°，
∴BE=1，AB=2，
∴DC=2，
作DF⊥BC于点F，
∴四边形AEFD是矩形，
∴AE=DF，
∵∠B=∠C，∠AEB=∠DFC=90°，
∴△ABE≌△DCF（AAS），
∴BE=FC=1，
∴EF=
-1，
∵AD∥BC，AE⊥BC，DF⊥BC，
∴AE∥DF，
∴四边形ADFE是平行四边形，
∴AD=EF=
-1，
∴梯形ABCD的周长为：AD+DC+BC+AB=
-1+2+2+2+
-1=4+2
．
答：梯形ABCD的周长是4+2
．
∴∠ACB=45°
∵AE⊥BC，AC=
| 6 |
∴AE=EC=
| 3 |
∵∠B=60°，
∴BE=1，AB=2，
∴DC=2，
作DF⊥BC于点F，
∴四边形AEFD是矩形，
∴AE=DF，
∵∠B=∠C，∠AEB=∠DFC=90°，
∴△ABE≌△DCF（AAS），
∴BE=FC=1，
∴EF=
| 3 |
∵AD∥BC，AE⊥BC，DF⊥BC，
∴AE∥DF，
∴四边形ADFE是平行四边形，
∴AD=EF=
| 3 |
∴梯形ABCD的周长为：AD+DC+BC+AB=
| 3 |
| 3 |
| 3 |
答：梯形ABCD的周长是4+2
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
