��Ŀ����
ͨ�������ǰѳ����κ�������ͳ��Ϊ���Σ���ͼ1����һ����Ϊ2a����Ϊ2b�ľ���ABCD�����Ѵ˾�����ͼ�е������ü�������Ϊ4��С�����Σ�Ȼ����ͼ2����״ƴ��һ��������MNPQ��
��1���ֱ������;ֲ��ĽǶȳ���������ͼ2����Ӱ���ֵ���������Եõ���ʽ��_________����
��2����ϸ�۲쳤����ABCD��������MNPQ�����Է������ǵ���_________����ͬ����_________����ͬ����ѡ��ܳ������������
��3�������������֣�������ۣ����ܳ�Ϊ36�����Χ��һ�����������������������ͬ��Χ��������Χ�����о����У�������ľ��ε��������_________����2��
��1���ֱ������;ֲ��ĽǶȳ���������ͼ2����Ӱ���ֵ���������Եõ���ʽ��_________����
��2����ϸ�۲쳤����ABCD��������MNPQ�����Է������ǵ���_________����ͬ����_________����ͬ����ѡ��ܳ������������
��3�������������֣�������ۣ����ܳ�Ϊ36�����Χ��һ�����������������������ͬ��Χ��������Χ�����о����У�������ľ��ε��������_________����2��

��1����a+b��2����a��b��2=4ab����2���ܳ����������3��81��
�����������1������������ڲ���С�����εı߳���Ȼ���ô������ε������ȥС�����ε����������Ӱ���ֵ�������Ӿֲ����ǣ�����ĸ�С���ε����������Ӱ���ֵ������
��2����ͼ2�������ͼ1�����������С�����ε�������ǣ�
��3�����ݣ�2���Ľ��ۣ��ܳ���ȵ�����£������ε�����Ⱦ��ε����������Χ�ɵ������ε�������Ȼ����������ν��м��㼴�ɣ�
�⣺��1�����忼�ǣ�����С�����εı߳�Ϊa��b��
����Ӱ���ֵ����=��a+b��2����a��b��2��
�ֲ����ǣ���Ӱ���ֵ����=4ab��
�ࣨa+b��2����a��b��2=4ab��
��2��ͼ1�ܳ�Ϊ��2��2a+2b��=4a+4b��
�����4ab��
ͼ2�ܳ�Ϊ��4��a+b��=4a+4b��
�����a+b��2=4ab+��a��b��2��4ab��
���ҽ���a=bʱȡ�Ⱥţ�
���ܳ���ͬ���������ͬ��
��3�����ݣ�2���Ľ��ۣ�Χ��������ʱ������
��ʱ���߳�Ϊ36��4=9�ף�
���=92=81��2��
�ʴ�Ϊ����1����a+b��2����a��b��2=4ab����2���ܳ����������3��81��
���������⿼������ȫƽ����ʽ�ļ��α��������ͼ�ε��ص㣬��������ҳ�����Ĺ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ����������������.
����������������. 
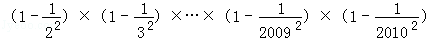 ��
�� x2+1��2��
x2+1��2��