题目内容
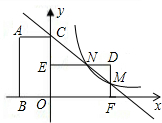
如图,矩形ABOC的边OB,OC分别在坐标轴上,将矩形ABOC绕原点O顺时针旋转90°后,得到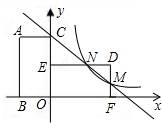 的矩形为DEOF.已知点A的坐标为(-2,m),反比例函数
的矩形为DEOF.已知点A的坐标为(-2,m),反比例函数 的图象(第一象限)经过线段DF的中点M,且满足m+n=6.
的图象(第一象限)经过线段DF的中点M,且满足m+n=6.
(1)求m,n的值;
(2)求直线CM的函数解析式;
(3)设直线CM交DE于点N,请判断点N是否在反比例函数 的图象上(写出理由).
的图象上(写出理由).
解:(1)∵将矩形ABOC绕原点O顺时针旋转90°后,得到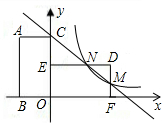 的矩形为DEOF,点A的坐标为(-2,m),
的矩形为DEOF,点A的坐标为(-2,m),
∴AC=BO=OE=DF=2,CO=OF=m,
∵反比例函数 的图象(第一象限)经过线段DF的中点M,
的图象(第一象限)经过线段DF的中点M,
∴M点的纵坐标为1,横坐标为:m,
∵M在反比例函数 的图象上,
的图象上,
∴xy=n=m,
∵m+n=6,
∴m=3,n=3;
(2)∵m=3,
∴C点坐标为:(0,3),M点坐标为:(3,1),
假设直线CM的函数解析式为:y=kx+b,
将C,M代入解析式得:
 ,
,
解得: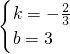 ,
,
故直线CM的函数解析式为: ;
;
(3)∵DE是平行于x轴的直线,且过(0,2)点,故直线DE可以表示为:y=2,
∴直线CM与直线DE交点N的坐标求法应该是将两直线解析式联立,求出公共解集,
故 ,
,
解得: ,
,
故N点的坐标为:( ,2),
,2),
∵ ×2=3,
×2=3,
∴点N在y= 上.
上.
分析:(1)由点A的坐标为(-2,m),得出矩形中AC=BO=OE=DF=2,再由反比例函数 的图象(第一象限)经过线段DF的中点M,得出M点的纵坐标为1,利用反比例函数的性质得出m,n的关系,进而求出m,n.
的图象(第一象限)经过线段DF的中点M,得出M点的纵坐标为1,利用反比例函数的性质得出m,n的关系,进而求出m,n.
(2)根据m,n的值即可求出C,M点的坐标,进而利用待定系数法求出直线解析式即可;
(3)利用两直线交点求法得出N点坐标,再代入反比例函数解析式即可得出点N是否在图象上.
点评:此题主要考查了反比例函数与一次函数的综合应用,根据M点的坐标以及反比例函数的性质xy=n,求出m=n是解决问题的关键.
 的矩形为DEOF,点A的坐标为(-2,m),
的矩形为DEOF,点A的坐标为(-2,m),∴AC=BO=OE=DF=2,CO=OF=m,
∵反比例函数
 的图象(第一象限)经过线段DF的中点M,
的图象(第一象限)经过线段DF的中点M,∴M点的纵坐标为1,横坐标为:m,
∵M在反比例函数
 的图象上,
的图象上,∴xy=n=m,
∵m+n=6,
∴m=3,n=3;
(2)∵m=3,
∴C点坐标为:(0,3),M点坐标为:(3,1),
假设直线CM的函数解析式为:y=kx+b,
将C,M代入解析式得:
 ,
,解得:
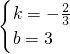 ,
,故直线CM的函数解析式为:
 ;
;(3)∵DE是平行于x轴的直线,且过(0,2)点,故直线DE可以表示为:y=2,
∴直线CM与直线DE交点N的坐标求法应该是将两直线解析式联立,求出公共解集,
故
 ,
,解得:
 ,
,故N点的坐标为:(
 ,2),
,2),∵
 ×2=3,
×2=3,∴点N在y=
 上.
上.分析:(1)由点A的坐标为(-2,m),得出矩形中AC=BO=OE=DF=2,再由反比例函数
 的图象(第一象限)经过线段DF的中点M,得出M点的纵坐标为1,利用反比例函数的性质得出m,n的关系,进而求出m,n.
的图象(第一象限)经过线段DF的中点M,得出M点的纵坐标为1,利用反比例函数的性质得出m,n的关系,进而求出m,n.(2)根据m,n的值即可求出C,M点的坐标,进而利用待定系数法求出直线解析式即可;
(3)利用两直线交点求法得出N点坐标,再代入反比例函数解析式即可得出点N是否在图象上.
点评:此题主要考查了反比例函数与一次函数的综合应用,根据M点的坐标以及反比例函数的性质xy=n,求出m=n是解决问题的关键.

练习册系列答案
相关题目
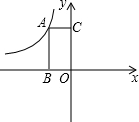 如图,矩形ABOC的面积为3,反比例函数y=
如图,矩形ABOC的面积为3,反比例函数y=| k |
| x |
| A、3 | B、-1.5 | C、-3 | D、-6 |
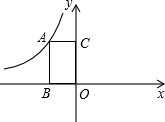
 如图,矩形ABOC的面积为2,反比例函数图象y=
如图,矩形ABOC的面积为2,反比例函数图象y=| k |
| x |
| A、2 | B、-2 | C、4 | D、-4 |
如图,矩形ABOC的面积为6,反比例函数y=
的图象经过点A,则k等于( )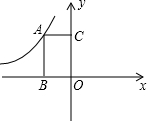
| k |
| x |

| A、6 | B、3 | C、-3 | D、-6 |
 的矩形为DEOF.已知点A的坐标为(-2,m),反比例函数
的矩形为DEOF.已知点A的坐标为(-2,m),反比例函数