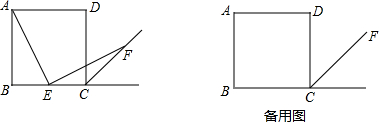��Ŀ����
��ͼ���ı���ABCD�У�AC=a��BD=b����AC�ABD��˳�������ı���ABCD �����е㣬�õ��ı���A1B1C1D1����˳�������ı���A1B1C1D1�����е㣬�õ��ı���A2B2C2D2������˽�����ȥ���õ��ı���AnBnCnDn�����н��� ��ȷ����
��ȷ����
���ı���A2B2C2D2�Ǿ��Σ���
���ı���A4B4C4D4�����Σ�
���ı���A5B5C5D5���ܳ���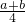
���ı���AnBnCnDn�������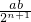 ��
��
- A.�٢�
- B.�ڢ�
- C.�ڢۢ�
- D.�٢ڢۢ�
C
���������ȸ������⣬�ҳ��仯����ı��εı߳����ı���ABCD�и��߳��ij��ȹ�ϵ���ɣ�Ȼ�������ѡ�������������жϣ�
�ٸ��ݾ��ε��ж������������жϣ�
�ڸ������ε��ж������������жϣ�
�����ı��ε��ܳ���ʽ���ܳ�=�߳�֮�ͣ��������ı���A5B5C5D5���ܳ���
�ܸ����ı���AnBnCnDn��������ı���ABCD��������������ϵ�����������
��� �⣺������A1C1��B1D1��
�⣺������A1C1��B1D1��
�����ı���ABCD�У�˳�������ı���ABCD �����е㣬�õ��ı���A1B1C1D1��
��A1D1��BD��B1C1��BD��C1D1��AC��A1B1��AC��
��A1D1��B1C1��A1B1��C1D1��
���ı���A1B1C1D1��ƽ���ı��Σ�
��AC�ABD�����ı���A1B1C1D1�Ǿ��Σ�
��B1D1=A1C1�����ε������Խ�����ȣ���
��A2D2=C2D2=C2B2=B2A2����λ�߶�������
���ı���A2B2C2D2�����Σ�
�ʱ�ѡ�����
���ɢ�֪���ı���A2B2C2D2�����Σ�
�������λ�߶���֪���ı���A4B4C4D4�����Σ�
�ʱ�ѡ����ȷ��
�۸�����λ�ߵ�������֪��A5B5= A3B3=
A3B3= ��
�� A1B1=
A1B1= ��
�� ��
�� AC��B5C5=
AC��B5C5= B3C3=
B3C3= ��
�� B1C1=
B1C1= ��
�� ��
�� BD��
BD��
���ı���A5B5C5D5���ܳ���2�� ��a+b��=
��a+b��=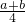 ��
��
�ʱ�ѡ����ȷ��
�ܡ��ı���ABCD�У�AC=a��BD=b����AC�ABD��
��S�ı���ABCD=ab��2��
�������ε���λ�ߵ����ʿ�����֪��ÿ�õ�һ���ı��Σ����������Ϊԭ����һ�룬
�ı���AnBnCnDn�������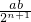 ��
��
�ʱ�ѡ����ȷ��
�����������ڢۢ���ȷ��
��ѡC��
������������Ҫ���������ε��ж������ʡ����ε��ж������ʼ������ε���λ�߶����������ε���λ��ƽ���ڵ������ҵ��ڵ����ߵ�һ�룩��������ʱ�����������Ρ�������ƽ���ı��εĹ�ϵ��
���������ȸ������⣬�ҳ��仯����ı��εı߳����ı���ABCD�и��߳��ij��ȹ�ϵ���ɣ�Ȼ�������ѡ�������������жϣ�
�ٸ��ݾ��ε��ж������������жϣ�
�ڸ������ε��ж������������жϣ�
�����ı��ε��ܳ���ʽ���ܳ�=�߳�֮�ͣ��������ı���A5B5C5D5���ܳ���
�ܸ����ı���AnBnCnDn��������ı���ABCD��������������ϵ�����������
���
 �⣺������A1C1��B1D1��
�⣺������A1C1��B1D1�������ı���ABCD�У�˳�������ı���ABCD �����е㣬�õ��ı���A1B1C1D1��
��A1D1��BD��B1C1��BD��C1D1��AC��A1B1��AC��
��A1D1��B1C1��A1B1��C1D1��
���ı���A1B1C1D1��ƽ���ı��Σ�
��AC�ABD�����ı���A1B1C1D1�Ǿ��Σ�
��B1D1=A1C1�����ε������Խ�����ȣ���
��A2D2=C2D2=C2B2=B2A2����λ�߶�������
���ı���A2B2C2D2�����Σ�
�ʱ�ѡ�����
���ɢ�֪���ı���A2B2C2D2�����Σ�
�������λ�߶���֪���ı���A4B4C4D4�����Σ�
�ʱ�ѡ����ȷ��
�۸�����λ�ߵ�������֪��A5B5=
 A3B3=
A3B3= ��
�� A1B1=
A1B1= ��
�� ��
�� AC��B5C5=
AC��B5C5= B3C3=
B3C3= ��
�� B1C1=
B1C1= ��
�� ��
�� BD��
BD�����ı���A5B5C5D5���ܳ���2��
 ��a+b��=
��a+b��=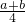 ��
���ʱ�ѡ����ȷ��
�ܡ��ı���ABCD�У�AC=a��BD=b����AC�ABD��
��S�ı���ABCD=ab��2��
�������ε���λ�ߵ����ʿ�����֪��ÿ�õ�һ���ı��Σ����������Ϊԭ����һ�룬
�ı���AnBnCnDn�������
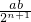 ��
���ʱ�ѡ����ȷ��
�����������ڢۢ���ȷ��
��ѡC��
������������Ҫ���������ε��ж������ʡ����ε��ж������ʼ������ε���λ�߶����������ε���λ��ƽ���ڵ������ҵ��ڵ����ߵ�һ�룩��������ʱ�����������Ρ�������ƽ���ı��εĹ�ϵ��

��ϰ��ϵ�д�
 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
�����Ŀ
 ��ͼ���ı���ABCD�ĶԽ���AC��BD���ഹֱƽ���ڵ�O����AC=2a��BD=2b�����Ƶ�����ı��ε����ʣ�������3����
��ͼ���ı���ABCD�ĶԽ���AC��BD���ഹֱƽ���ڵ�O����AC=2a��BD=2b�����Ƶ�����ı��ε����ʣ�������3���� ��ͼ���ı���ABCD�ĶԽ���AC��BD���ڵ�P������P��ֱ�߽�AD�ڵ�E����BC�ڵ�F����PE=PF����AP+AE=CP+CF��
��ͼ���ı���ABCD�ĶԽ���AC��BD���ڵ�P������P��ֱ�߽�AD�ڵ�E����BC�ڵ�F����PE=PF����AP+AE=CP+CF��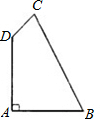 ��ͼ���ı���ABCD��AB=AD=2��BC=3��CD=1����A=90�㣬���ADC�Ķ�����
��ͼ���ı���ABCD��AB=AD=2��BC=3��CD=1����A=90�㣬���ADC�Ķ�����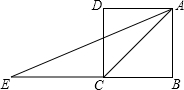 ��ͼ���ı���ABCDΪ�����Σ�E��BC���ӳ����ϵ�һ�㣬��AC=CE�����DAE�Ķ�����
��ͼ���ı���ABCDΪ�����Σ�E��BC���ӳ����ϵ�һ�㣬��AC=CE�����DAE�Ķ�����