题目内容
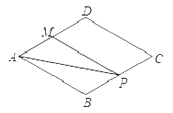
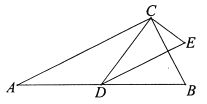
【题目】 在矩形ABCD中,AB=3,AD=4,点P为AB边上的动点(P与A、B不重合),将△BCP沿CP翻折,点B的对应点B1在矩形外,PB1交AD于E,CB1交AD于点F.
(1)如图1,求证:△APE∽△DFC;
(2)如图1,如果EF=PE,求BP的长;
(3)如图2,连接BB′交AD于点Q,EQ:QF=8:5,求tan∠PCB.

【答案】(1)见解析;(2)BP=2.4;(3)tan∠PCB=![]() .
.
【解析】
(1)由矩形的性质可得∠A=∠D=∠ABC=∠BCD=90°,由余角的性质和对顶角的性质可得∠DFC=∠APE,即可得结论;
(2)由题意可证△APE≌△B1FE,可得AE=B1E,AP=B1F,即AF=B1P,由折叠的性质可得BP=B1P=a,BC=B1C=4,根据勾股定理可求BP的长.
(3)由折叠的性质和等腰三角形的性质可得∠PB1B=∠PCB,设EQ=8k,QF=5k,可得B1F=5k,EF=EQ+QF=13k,由勾股定理可得B1E=12k,由相似三角形的性质可得EH=![]() ,HQ=
,HQ=![]() ,即可求tan∠PCB.
,即可求tan∠PCB.
(1)∵四边形ABCD是矩形
∴∠A=∠D=∠ABC=∠BCD=90°
∴∠APE+∠AEP=90°,∠DCF+∠DFC=90°,
∵折叠
∴∠ABC=∠PB1C=90°,
∴∠B1EF+∠B1FE=90°,
又∵∠B1EF=∠AEP,∠B1FE=∠DFC,
∴∠DFC=∠APE,且∠A=∠D,
∴△APE∽△DFC
(2)∵PE=EF,∠A=∠B1=90°,∠AEP=∠B1EF,
∴△APE≌△B1FE(AAS),
∴AE=B1E,AP=B1F,
∴AE+EF=PE+B1E,
∴AF=B1P,
设BP=a,则AP=3﹣a=B1F,
∵折叠
∴BP=B1P=a,BC=B1C=4,
∴AF=a,CF=4﹣(3﹣a)=a+1
∴DF=AD﹣AF=4﹣a,
在Rt△DFC中,CF2=DF2+CD2,
∴(a+1)2=(4﹣a)2+9,
∴a=2.4
即BP=2.4
(3)∵折叠
∴BC=B1C,BP=B1P,∠BCP=∠B1CP,
∴CP垂直平分BB1,
∴∠B1BC+∠BCP=90°,
∵BC=B1C,
∴∠B1BC=∠BB1C,且∠BB1C+∠PB1B=90°
∴∠PB1B=∠PCB,
∵四边形ABCD是矩形
∴AD∥BC
∴∠B1BC=∠B1QF,
∴∠B1QF=∠BB1C,
∴QF=B1F
∵EQ:QF=8:5,
∴设EQ=8k,QF=5k,
∴B1F=5k,EF=EQ+QF=13k,
在Rt△B1EF中,B1E=![]() =12k,
=12k,
如图,过点Q作HQ⊥B1E于点H,
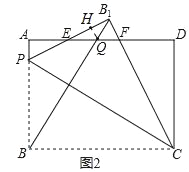
又∵∠PB1C=90°,
∴HQ∥B1F
∴△EHQ∽△EB1F,
∴![]() =
=![]() =
=![]()
∴![]() =
=![]() =
=![]()
∴EH=![]() ,HQ=
,HQ=![]()
∴B1H=![]()
∴tan∠PCB=tan∠PB1B=![]() =
=![]()

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案