ЬтФПФкШн
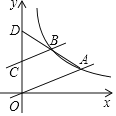
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпyЃНmx2Љ2mx+m+4гыyжсНЛгкЕуAЃЈ0ЃЌ3ЃЉЃЌгыxжсНЛгкЕуBЃЌCЃЈЕуBдкЕуCзѓВрЃЉЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФБэДяЪНМАЕуBЃЌCЕФзјБъЃЛ
ЃЈ2ЃЉХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуDЃЌШєжБЯпyЃНkx+bОЙ§ЕуDКЭЕуEЃЈЉ1ЃЌЉ2ЃЉЃЌЧѓжБЯпDEЕФБэДяЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌвбжЊЕуPЃЈtЃЌ0ЃЉЃЌЙ§ЕуPзїДЙжБгкxжсЕФжБЯпНЛХзЮяЯпгкЕуMЃЌНЛжБЯпDEгкЕуNЃЌШєЕуMКЭЕуNжажСЩйгавЛИіЕудкxжсЯТЗНЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌB(-1,0)ЃЌC(3,0)ЃЛЃЈ2ЃЉy=x-1ЃЛЃЈ3ЃЉ
ЃЌB(-1,0)ЃЌC(3,0)ЃЛЃЈ2ЃЉy=x-1ЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉгЩХзЮяЯп![]() гыyжсНЛгкЕуAЃЈ0,3ЃЉЃЌАбAЕузјБъДњШыНтЮіЪНПЩЕУГіmЕФжЕЃЌМДЧѓГіХзЮяЯпЕФНтЮіЪНЃЌШЛКѓХзЮяЯпгы
гыyжсНЛгкЕуAЃЈ0,3ЃЉЃЌАбAЕузјБъДњШыНтЮіЪНПЩЕУГіmЕФжЕЃЌМДЧѓГіХзЮяЯпЕФНтЮіЪНЃЌШЛКѓХзЮяЯпгы![]() жсНЛгкЕуBЁЂCСНЕуЃЌМДПЩЧѓГіBЁЂCСНЕуЕФзјБъЃЛЃЈ2ЃЉ
жсНЛгкЕуBЁЂCСНЕуЃЌМДПЩЧѓГіBЁЂCСНЕуЕФзјБъЃЛЃЈ2ЃЉ
ЃЈ2ЃЉгЩ![]() ЧѓГіЕуDЕФзјБъЃЌНЋDКЭEЕФЕуДњШыжБЯп
ЧѓГіЕуDЕФзјБъЃЌНЋDКЭEЕФЕуДњШыжБЯп![]() ЕФНтЮіЪНЃЌМДПЩЧѓГіжБЯпDEЕФБэДяЪНЃЛ
ЕФНтЮіЪНЃЌМДПЩЧѓГіжБЯпDEЕФБэДяЪНЃЛ
ЃЈ3ЃЉИљОнЭМЯёМДПЩжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЁпХзЮяЯп![]() гыyжсНЛгкЕуAЃЈ0,3ЃЉЃЌ
гыyжсНЛгкЕуAЃЈ0,3ЃЉЃЌ
Ёрm+4=3ЃЎ
Ёрm=-1ЃЎ
ЁрХзЮяЯпЕФБэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЁпХзЮяЯп![]() гы
гы![]() жсНЛгкЕуBЃЌCЃЌ
жсНЛгкЕуBЃЌCЃЌ
ЁрСюy=0ЃЌМД![]() ЃЎ
ЃЎ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
гжЁпЕуBдкЕуCзѓВрЃЌ
ЁрЕуBЕФзјБъЮЊ![]() ЃЌЕуCЕФзјБъЮЊ
ЃЌЕуCЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЁп![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЎ
ЃЎ
ЁпХзЮяЯпЕФЖдГЦжсгы![]() жсНЛгкЕуDЃЌ
жсНЛгкЕуDЃЌ
ЁрЕуDЕФзјБъЮЊ(1,0)ЃЎ
ЁпжБЯп![]() ОЙ§ЕуD(1,0)КЭЕуE(-1,-2)ЃЌ
ОЙ§ЕуD(1,0)КЭЕуE(-1,-2)ЃЌ
Ёр![]()
НтЕУ![]()
ЁржБЯпDEЕФБэДяЪНЮЊy=x-1ЃЎ
ЃЈ3ЃЉ![]() Лђ
Лђ![]()

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ