题目内容
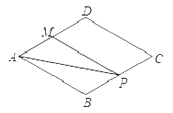
【题目】如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )
A. 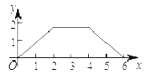 B.
B. 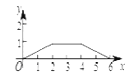 C.
C. 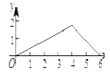 D.
D. 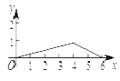
【答案】A
【解析】
分类讨论:当0≤x≤2,如图1,作PH⊥AD于H,AP=x,根据菱形的性质得∠A=60°,AM=1,则∠APH=30°,根据含30度的直角三角形三边的关系得到在RtAH=![]() x,PH=
x,PH=![]() x,然后根据三角形面积公式得y=
x,然后根据三角形面积公式得y=![]() AMPH=
AMPH=![]() x;当2<x≤4,如图2,作BE⊥AD于E,AP+BP=x,根据菱形的性质得∠A=60°,AM=1,AB=2,BC∥AD,则∠ABE=30°,在Rt△ABE中,根据含30度的直角三角形三边的关系得AE=1,PH=
x;当2<x≤4,如图2,作BE⊥AD于E,AP+BP=x,根据菱形的性质得∠A=60°,AM=1,AB=2,BC∥AD,则∠ABE=30°,在Rt△ABE中,根据含30度的直角三角形三边的关系得AE=1,PH=![]() ,然后根据三角形面积公式得y=
,然后根据三角形面积公式得y=![]() AMBE=
AMBE=![]() ;
;
当4<x≤6,如图3,作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,根据菱形的性质得∠ADC=120°,则∠DPF=30°,在Rt△DPF中,根据含30度的直角三角形三边的关系得DF=![]() (6-x),PF=
(6-x),PF=![]() DF=
DF=![]() (6-x),则利用三角形面积公式得y=
(6-x),则利用三角形面积公式得y=![]() AMPF=-
AMPF=-![]() x+
x+![]() ,最后根据三个解析式和对应的取值范围对各选项进行判断.
,最后根据三个解析式和对应的取值范围对各选项进行判断.
当点P在AB上运动时,即0≤x≤2,如图1,
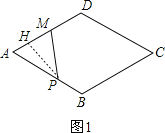
作PH⊥AD于H,AP=x,
∵菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,
∴∠A=60°,AM=1,
∴∠APH=30°,
在Rt△APH中,AH=![]() AP=
AP=![]() x,
x,
PH=![]() AH=
AH=![]() x,
x,
∴y=![]() AMPH=
AMPH=![]() ×1×
×1×![]() x=
x=![]() x;
x;
当点P在BC上运动时,即2<x≤4,如图2,
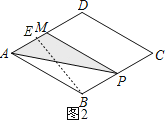
作BE⊥AD于E,AP+BP=x,
∵四边形ABCD为菱形,∠B=120°,
∴∠A=60°,AM=1,AB=2,BC∥AD,
∴∠ABE=30°,
在Rt△ABE中,AE=![]() AB=1,
AB=1,
PH=![]() AE=
AE=![]() ,
,
∴y=![]() AMBE=
AMBE=![]() ×1×
×1×![]() =
=![]() ;
;
当点P在CD上运动时,即4<x≤6,如图3,
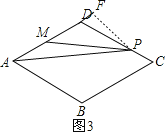
作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,
∵菱形ABCD中,∠B=120°,
∴∠ADC=120°,
∴∠DPF=30°,
在Rt△DPF中,DF=![]() DP=
DP=![]() (6-x),
(6-x),
PF=![]() DF=
DF=![]() (6-x),
(6-x),
∴y=![]() AMPF=
AMPF=![]() ×1×
×1×![]() (6-x)=
(6-x)=![]() (6-x)=-
(6-x)=-![]() x+
x+![]() ,
,
∴△APM的面积y与点P经过的路程x之间的函数关系的图象为三段:当0≤x≤2,图象为线段,满足解析式y=![]() x;当2≤x≤4,图象为平行于x轴的线段,且到x轴的距离为
x;当2≤x≤4,图象为平行于x轴的线段,且到x轴的距离为![]() ;当4≤x≤6,图象为线段,且满足解析式y=-
;当4≤x≤6,图象为线段,且满足解析式y=-![]() x+
x+![]() .
.
故选B.