题目内容
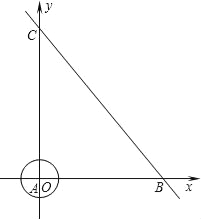
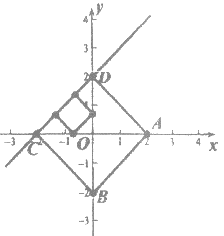
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.例如:如图l,正方形ABCD是一次函数![]() 图象的其中一个伴侣正方形.
图象的其中一个伴侣正方形.
(1)若某函数是一次函数![]() ,直接写出它的图象的所有伴侣正方形的边长;
,直接写出它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数![]() (k>0),它的图象的伴侣正方形为ABCD,点D(3,m)(m<3)在这个反比例函数图象上,求m的值及反比例函数解析式;
(k>0),它的图象的伴侣正方形为ABCD,点D(3,m)(m<3)在这个反比例函数图象上,求m的值及反比例函数解析式;
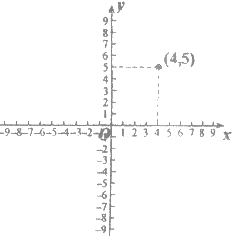
(3)若某函数是二次函数![]() (a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(4,5).直接写出所有伴侣正方形在抛物线上的另一个顶点坐标及相应的抛物线解析式.
(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(4,5).直接写出所有伴侣正方形在抛物线上的另一个顶点坐标及相应的抛物线解析式.
【答案】(1)![]() 或2
或2![]() ;(2)m的值为
;(2)m的值为![]() ,反比例函数解析式为
,反比例函数解析式为![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)先正确地画出图形,再利用正方形的性质确定相关点的坐标从而计算正方形的边长,注意思维的严密性.
(2)因为ABCD为正方形,所以可作垂线得到等腰直角三角形,利用点D(2,m)的坐标表示出点C的坐标从而求解.
(3)注意思维的严密性,抛物线开口既可能向上,也可能向下.当抛物线开口向上时,正方形的另一个顶点也是在抛物线上,这个点既可能在点(4,5)的左边,也可能在点(4,5)的右边,过点(4,5)向x轴作垂线,利用全等三角形确定线段的长即可确定抛物线上另一个点的坐标;当抛物线开口向下时也是一样地分为两种情况来讨论.
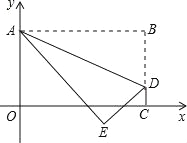
(1)(I)当点A在x轴正半轴、点B在y轴负半轴上时:
正方形ABCD的边长为![]() .
.
(II)当点A在x轴负半轴、点B在y轴正半轴上时:
设正方形边长为a,易得![]()
解得a=![]() ,此时正方形的边长为
,此时正方形的边长为![]() .
.
∴所求“伴侣正方形”的边长为![]() 或
或![]() ;
;
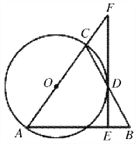
(2)如图,作DE⊥x轴,CF⊥y轴,垂足分别为点E.F,
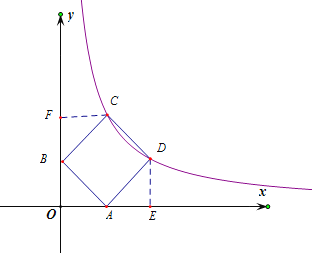
易证△ADE≌△BAO≌△CBF.
∵点D的坐标为(3,m),m<3,
∴DE=OA=BF=m,
∴OB=AE=CF=3m.
∴OF=BF+OB=3,
∴点C的坐标为(3m,3).
∴3m=3(3m),解得m=![]() .
.
∴反比例函数的解析式为![]() .
.
(3)另一个顶点坐标为(9,-4),抛物线解析式为![]() ;
;
另一个顶点坐标为(-l,4),抛物线解析式为![]() ;
;
另一个顶点坐标为(-5,9),抛物线解析式为![]() ;
;
另一个顶点坐标为(5,1),抛物线解析式为![]() .
.