题目内容
【题目】如图,平面直角坐标系中,![]() 的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.
的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.
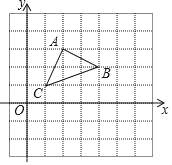
(1)![]() 的形状是 (直接写答案)
的形状是 (直接写答案)
(2)画出![]() 沿
沿![]() 轴翻折后的
轴翻折后的![]() ;
;
(3)画出![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 的
的![]() 并求出旋转过程中
并求出旋转过程中![]() 扫过的面积.(结果保留
扫过的面积.(结果保留![]() )
)
【答案】(1)等腰直角三角形;(2)画图见解析;(3)![]()
【解析】
(1)根据勾股定理及其逆定理即可判断;
(2)分别作出三顶点关于x轴的对称点,再顺次连接可得答案;
(3)作出点A,C绕点B顺时针旋转90°的对应点,再顺次连接可得:旋转过程中三角形扫过的面积是三角形面积与扇形的面积和,据此列式计算.
(1)∵AB2=12+22=5,AC2=12+22=5,BC2=12+32=10,∴AB2+AC2=BC2,且AB=AC,∴△ABC是等腰直角三角形.
故答案为:等腰直角三角形;
(2)如图,△A1B1C1即为所求.
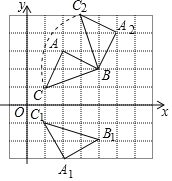
(3)如图,△BA2C2即为所求,△ABC扫过的面积为![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目