题目内容
【题目】在矩形ABCD中,AD=8,AB=6,点E为射线DC上一个动点,把△ADE沿AE折叠,使点D落在点F处,若△CEF为直角三角形时,DE的长为 . 
【答案】![]() 或8
或8
【解析】解:∵四边形ABCD是矩形, ∴∠D=∠B=90°,CD=AB=6,
∴AC= ![]() =
= ![]() =10,
=10,
当△CEF为直角三角形时,有两种情况:
①当点F落在矩形内部时,F落在AC上,如图1所示.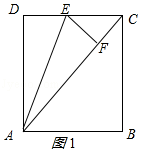
由折叠的性质得:EF=DE,AF=AD=8,
设DE=x,则EF=x,CE=6﹣x,
∴CE=6﹣x,
在Rt△CEF中,由勾股定理得:
∵EF2+CF2=CE2 ,
∴x2+22=(6﹣x)2 ,
解得x= ![]() ,
,
∴DE= ![]() ;
;
②当点F落在AB边上时,如图2所示.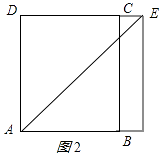
此时ADEF为正方形,
∴DE=AD=8.
③当点F落在AB边上时,易知BF= ![]() =2
=2 ![]() ,设DE=EF=x,
,设DE=EF=x,
在Rt△EFC中,x2=(6﹣x)2+(8﹣2 ![]() )2 ,
)2 ,
∴x= ![]() ,
,
∴DE= ![]() ,
,
综上所述,BE的长为 ![]() 或8或
或8或 ![]() .
.
所以答案是: ![]() 或8.
或8.
【考点精析】根据题目的已知条件,利用矩形的性质和翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

【题目】为建设生态平顶山,某校学生在植树节那天,组织九年级八个班的学生到山顶公园植树,各班植树情况如下表:下列说法错误的是( )
班 级 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 |
棵 数 | 15 | 18 | 22 | 25 | 29 | 14 | 18 | 19 |
A.这组数据的众数是18
B.这组数据的平均数是20
C.这组数据的中位数是18.5
D.这组数据的方差为0
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.




