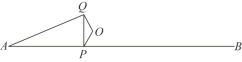ЬтФПФкШн
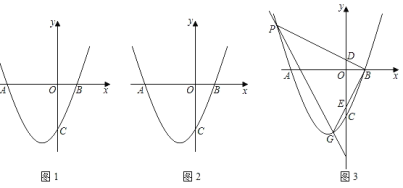
ЁОЬтФПЁПШчЭМ1ЃЌИУХзЮяЯпЪЧгЩyЃНx2ЦНвЦКѓЕУЕНЃЌЫќЕФЖЅЕузјБъЮЊЃЈЉ![]() ЃЌЉ
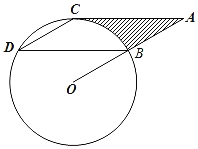
ЃЌЉ![]() ЃЉЃЌВЂгызјБъжсЗжБ№НЛгкAЃЌBЃЌCШ§ЕуЃЎ
ЃЉЃЌВЂгызјБъжсЗжБ№НЛгкAЃЌBЃЌCШ§ЕуЃЎ
ЃЈ1ЃЉЧѓAЃЌBЕФзјБъЃЎ
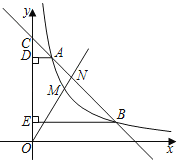
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгBCЃЌACЃЌдкЕкШ§ЯѓЯоЕФХзЮяЯпЩЯгавЛЕуPЃЌЪЙЁЯPCAЃНЁЯBCOЃЌЧѓЕуPЕФзјБъЃЎ
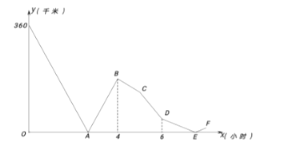
ЃЈ3ЃЉШчЭМ3ЃЌжБЯпyЃНax+bЃЈbЃМ0ЃЉгыИУХзЮяЯпЗжБ№НЛгкPЃЌGСНЕуЃЌСЌНгBPЃЌBGЗжБ№НЛyжсгкЕуDЃЌEЃЎШєODOEЃН3ЃЌЧыЬНЫїaгыbЕФЪ§СПЙиЯЕЃЎВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉbЃН4a+3ЃЌРэгЩМћНтЮіЃЎ
ЃЛЃЈ3ЃЉbЃН4a+3ЃЌРэгЩМћНтЮіЃЎ
ЁОНтЮіЁП
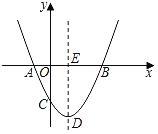
ЃЈ1ЃЉИљОнЖЅЕузјБъаДГіЖЅЕуЪНЃЌЛЏЖЅЕуЪНЮЊвЛАуЪНЃЌЗжБ№Сюx=0Лђy=0МДПЩЧѓГіAЁЂBЕФзјБъЃЛ
ЃЈ2ЃЉжБЯпCPНЛxжсгкЕуHЃЌЙЪЕуHзїHGЁЭACНЛACЕФбгГЄЯпгкЕуGЃЌИљОнtanЁЯBCOЃНtanЁЯPCAНтжБНЧШ§НЧаЮМДПЩЧѓГіHЕузјБъЃЌгЩДЫПЩЧѓЕУжБЯпCHЕФБэДяЪНЃЌСЊСЂЖўДЮКЏЪ§НтЮіЪНМДПЩЧѓЕУЕуPзјБъЃЛ
ЃЈ3ЃЉжБЯпBPЕФБэДяЪНЮЊЃКy=ЃЈm+4ЃЉx-ЃЈm+4ЃЉЁЂжБЯпBGЕФБэДяЪНЮЊЃКy=ЃЈn+4ЃЉx-ЃЈn+4ЃЉЃЌЙЪOD=-ЃЈm+4ЃЉЃЌOE=ЃЈn+4ЃЉЃЌODOE=-ЃЈm+4ЃЉЃЈn+4ЃЉ=3ЃЌМД-[mn+4ЃЈm+nЃЉ+16]=3ЃЌЖјm+n=a-3ЃЌmn=-b-4ЃЌМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉХзЮяЯпЕФБэДяЪНЮЊЃКyЃНЃЈx+![]() ЃЉ2Љ
ЃЉ2Љ![]() ЃНx2+3xЉ4ЁЂйЃЌ
ЃНx2+3xЉ4ЁЂйЃЌ
СюxЃН0ЃЌдђyЃНЉ4ЃЌЙЪЕуCЃЈ0ЃЌЉ4ЃЉЃЛ
СюyЃН0ЃЌдђxЃН-4Лђ1ЃЌ
ЙЪЕуAЁЂBЕФзјБъЗжБ№ЮЊЃКЃЈЉ4ЃЌ0ЃЉЁЂЃЈ1ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉШчЭМЃЌЩшжБЯпCPНЛxжсгкЕуHЃЌЙЪЕуHзїHGЁЭACНЛACЕФбгГЄЯпгкЕуGЃЌ
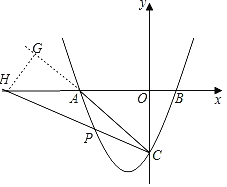
tanЁЯBCOЃН![]() ЃН
ЃН![]() ЃНtanЁЯPCAЃЌ
ЃНtanЁЯPCAЃЌ
ЁпOAЃНOCЃН4ЃЌЙЪЁЯBACЃН45ЁуЃНЁЯGAHЃЌ
ЩшGHЃНGAЃНxЃЌдђGCЃН4xЃЌЙЪACЃНGCЉGAЃН3xЃН4![]() ЃЌ
ЃЌ
НтЕУЃКxЃН![]() ЃЌ
ЃЌ
дђAHЃН![]() xЃН
xЃН![]() ЃЌЙЪЕуHЃЈЉ
ЃЌЙЪЕуHЃЈЉ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЩшCHЕФБэДяЪНЮЊЃКyЃНkx+bЃЌ
НЋCЁЂHЕФзјБъДњШыЕУ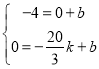 ЃЌНтЕУ
ЃЌНтЕУ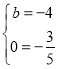 ЃЌ
ЃЌ
ЁрCHЕФБэДяЪНЮЊЃКyЃНЉ![]() xЉ4ЁЂкЃЌ
xЉ4ЁЂкЃЌ
СЊСЂЂйЂкВЂНтЕУЃКxЃН0ЃЈЩсШЅЃЉЛђ![]() ЃЌ
ЃЌ
ЙЪЕуPЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЩшЕуPЁЂGЕФзјБъЗжБ№ЮЊЃКЃЈmЃЌm2+3mЉ4ЃЉЁЂЃЈnЃЌn2+3nЉ4ЃЉЃЌ
гЩЕуPЁЂBЕФзјБъЕУЃЌжБЯпPBЕФБэДяЪНЮЊЃКyЃНЃЈm+4ЃЉxЉЃЈm+4ЃЉЃЛ
ЭЌРэжБЯпBGЕФБэДяЪНЮЊЃКyЃНЃЈn+4ЃЉxЉЃЈn+4ЃЉЃЛ
ЙЪODЃНЉЃЈm+4ЃЉЃЌOEЃНЃЈn+4ЃЉЃЌ
жБЯпyЃНax+bЃЈbЃМ0ЃЉЁЂлЃЌ
СЊСЂЂйЂлВЂећРэЕУЃКx2+ЃЈ3ЉaЃЉxЉbЉ4ЃН0ЃЌ
ЙЪm+nЃНaЉ3ЃЌmnЃНЉbЉ4ЃЌ
ODOEЃНЉЃЈm+4ЃЉЃЈn+4ЃЉЃН3ЃЌ
МДЉ[mn+4ЃЈm+nЃЉ+16]ЃН3ЃЌЖјm+nЃНaЉ3ЃЌmnЃНЉbЉ4ЃЌ
ећРэЕУЃКbЃН4a+3ЃЎ