题目内容
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
(1)当α=60°时,判断点B是否在直线O′B′上,并说明理由;
(2)连接OO′,设OO′与AB交于点D,当α为何值时,四边形ADO′B′是平行四边形?请说明理由.
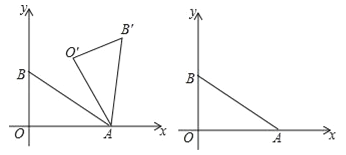
【答案】(1)点B(0,1)在直线O′B′上;(2)当α=120°时,四边形ADO′B′是平行四边形.
【解析】
试题分析:(1)首先证明∠BAO=30°,再求出直线O′B′的解析式即可解决问题.
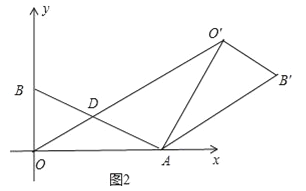
(2)如图2中,当α=120°时,四边形ADO′B′是平行四边形.只要证明∠DAO′=∠AO′B′=90°,∠O′AO=∠O′AB′=30°,即可解决问题.
试题解析:解;(1)如图1中,∵一次函数![]() 的图象与x轴、y轴分别交于点A、B,∴A(
的图象与x轴、y轴分别交于点A、B,∴A(![]() ,0),B(0,1),∴tan∠BAO=
,0),B(0,1),∴tan∠BAO=![]() ,∴∠BAO=30°,AB=2OB=2,∵旋转角为60°,∴B′(
,∴∠BAO=30°,AB=2OB=2,∵旋转角为60°,∴B′(![]() ,2),O′(
,2),O′(![]() ,
,![]() ),设直线O′B′解析式为y=kx+b,∴,
),设直线O′B′解析式为y=kx+b,∴,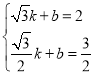 ,解得:
,解得: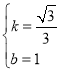 ,∴直线O′B′的解析式为
,∴直线O′B′的解析式为![]() ,∵x=0时,y=1,∴点B(0,1)在直线O′B′上.
,∵x=0时,y=1,∴点B(0,1)在直线O′B′上.
(2)如图2中,当α=120°时,四边形ADO′B′是平行四边形.
理由:∵AO=AO′,∠OAO′=120°,∠BAO=30°,∴∠DAO′=∠AO′B′=90°,∠O′AO=∠O′AB′=30°,∴AD∥O′B′,DO′∥AB′,∴四边形ADO′B′是平行四边形.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目