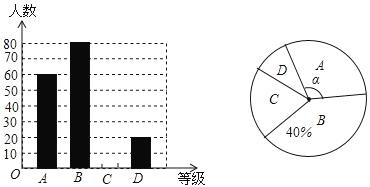
题目内容
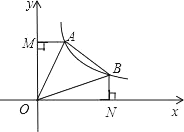
【题目】如图,在Rt△ABC中,∠C=90°,AC=5,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,![]() ,则BC边的长为_.
,则BC边的长为_.
【答案】3
【解析】
作EQ⊥x轴,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,5).设B(x,0),由于O点为以AB一边向三角形外作正方形ABEF的中心,利用AAS得到三角形ABC与三角形BEQ全等,利用全等三角形的对应边相等得到AC=BQ=5,BC=EQ,设BC=EQ=x,由OM为梯形ACQE的中位线,利用梯形中位线定理表示出OM,再由CM,表示出O坐标,进而表示出OC的长,根据已知OC的长列出关于x的方程,求出方程的解得到x的值,即可确定出BC的长.
解:作EQ⊥x轴,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,5).
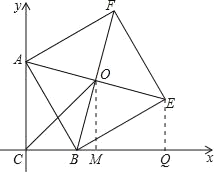
设B(x,0),由于O点为以AB一边向三角形外作正方形ABEF的中心,
∴AB=BE,∠ABE=90°,
∵∠ACB=90°,
∴∠BAC+∠ABC=90°,∠ABC+∠EBQ=90°,
∴∠BAC=∠EBQ,
在△ABC和△BEQ中,
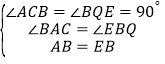 ,
,
∴△ACB≌△BQE(AAS),
∴AC=BQ=5,BC=EQ,
设BC=EQ=x,
∴O为AE中点,
∴OM为梯形ACQE的中位线,
∴OM=![]() ,
,
又∵CM=![]() CQ=
CQ=![]() ,
,
∴O点坐标为(![]() ,
,![]() ),
),
根据题意得:OC=4![]() =
=![]() ,
,
解得:x=3,
则BC=3.
故答案为:3.

练习册系列答案
相关题目