题目内容
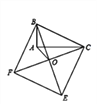
【题目】如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=3,AO=![]() ,那么AC的长等于( )
,那么AC的长等于( )
A. 7 B. 8 C. ![]() D.
D. ![]()
【答案】A
【解析】在AC上截取CG=AB=2,连接OG,根据B、A、O、C四点共圆,推出∠ABO=∠ACO,证△BAO≌△CGO,推出OA=OG=2![]() ,∠AOB=∠COG,得出等腰直角三角形AOG,根据勾股定理求出AG,即可求出AC.
,∠AOB=∠COG,得出等腰直角三角形AOG,根据勾股定理求出AG,即可求出AC.
在AC上截取CG=AB=2,连接OG,
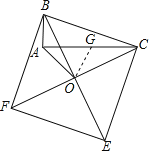
∵四边形BCEF是正方形,∠BAC=90°,
∴OB=OC,∠BAC=∠BOC=90°,
∴B、A、O、C四点共圆,
∴∠ABO=∠ACO,
在△BAO和△CGO中
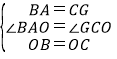 ,
,
∴△BAO≌△CGO(SAS),
∴OA=OG=2![]() ,∠AOB=∠COG,CG=AB=3
,∠AOB=∠COG,CG=AB=3
∵∠BOC=∠COG+∠BOG=90°,
∴∠AOG=∠AOB+∠BOG=90°,
即△AOG是等腰直角三角形,
由勾股定理得:AG=![]() =4,
=4,
即AC=4+3=7,
故选:A.

 学业测评一课一测系列答案
学业测评一课一测系列答案【题目】在某书店准备购进甲、乙两种图书共100本,购书款不高于2224元,两种图书的进价、售价如下表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 16 | 28 |
售价(元/本) | 26 | 40 |
请解答下列问题:
(1)在这批图书全部售出的条件下,书店如何进货利润最大?最大利润是多少?
(2)书店计划用(1)中的最大利润购买单价分别为72元、96元的排球、篮球捐给贫困山区的学校,那么在钱恰好用尽的情况下,最多可以购买排球和篮球共多少个?
【题目】在“朗读者”节目的影响下,某中学在暑期开展了“好书伴我成长”读书话动,并要求读书要细读,最少要读完2本书,最多不建议超过5本。初一年级5个班,共200名学生,李老师为了了解学生暑期在家的读书情况,给全班同学布置了一项调查作业:了解初一年级学生暑期读书情况.班中三位同学各自对初一年级读书情况进行了抽样调查,并将数据进行了整理,绘制的统计图表分别为表1、表2、表3.
表1:在初一年级随机选择5名学生暑期读书情况的统计表
阅读书数量(本) | 2 | 3 | 4 | 5 |
人数 | 2 | 1 | 1 | 1 |
表2:在初一年级“诵读班”班随机选取20名学生暑期读书情况的统计表
阅读书数量(本) | 2 | 3 | 4 | 5 |
人数 | 0 | 1 | 4 | 15 |
表3:在初一年级随机选取20名学生暑期读书情况的统计表
阅读书数量(本) | 2 | 3 | 4 | 5 |
人数 | 2 | 8 | 6 | 4 |
问题1:根据以上材料回答:三名同学中,哪一位同学的样本选取更合理,并简要说明其他两位同学选取样本的不足之处;
老师又对合理样本中的所有学生进行了“阅读动机”的调研,并制作成了如下统计图.
问题2:通过统计图的信息你认为“阅读动机”
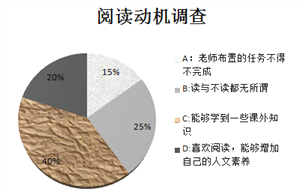
在“40%”的群体,暑期读几本书的可能性大,并说出你的理由.
【题目】食品厂从生产的袋装食品中抽出样品![]() 袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负来表示,记录如下表;
袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负来表示,记录如下表;
与标准质量的差值(单位:克) |
|
|
|
|
|
|
袋数 |
|
|
|
|
|
|
(1)这批样品的平均质量比标准质量是超过还是不足?平均每袋超过或不足多少克?
(2)若每袋标准质量为![]() 克,求抽样检测的样品总质量是多少?
克,求抽样检测的样品总质量是多少?