Question

【题目】正方形中，点是上一点，过点作交射线于点，连结．

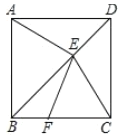
（1）已知点在线段上.

①若，求度数；

②求证：.

（2）已知正方形边长为，且，请直接写出线段的长．

Answer 1

【答案】（1）①；②见解析；（2）的长为或

【解析】

(1) ①根据正方形性质，求出；根据等腰三角形性质，求出的度数，即可求得.

②根据正方形对称性得到；根据四边形内角和证出；利用等角对等边即可证出.

（2）分情况讨论：①当点F在线段BC上时; ②当点F在线段CB延长线上时;根据正方形的对称性，证出；再根据等腰三角形的性质，求出线段NC，BN；利用勾股定理，求出BE、BD，进而求出DE.

解：（1）①为正方形，

．

又，

．

②证明：正方形关于对称，

，

．

又，

又

，

，

．

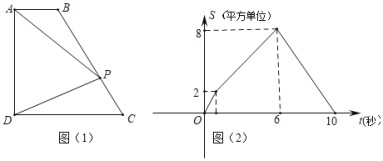
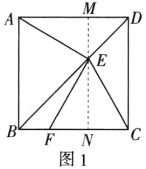
（2）①当点F在线段BC上时，过E作MN⊥BC，垂足为N，交AD于M，如图1所示：

∴N是CF的中点，

∴BF=1，∴CF=1

又∵四边形CDMN是矩形

∴为等腰直角三角形

∴

②当点F在线段CB延长线上时，如图2所示：

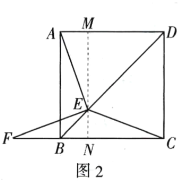
过点E作MN⊥BC，垂足为N，交AD于M

∵正方形ABCD关于BD对称

又∵

又

∴FC=3

∴

∴

∴ ,

综上所述，的长为或