题目内容
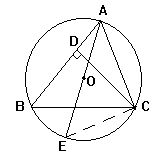
如图，△ABC内接于⊙O，AE是⊙O的直径，CD是△ABC中AB边上的高，
求证：AC·BC=AE·CD
求证：AC·BC=AE·CD
.证明，连结EC，∵AE是直径
∴∠ACE=∠D=Rt∠
∠B=∠E
∴△BDC∽△ECA
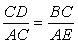
即AC·BC=AE·CD
∴∠ACE=∠D=Rt∠
∠B=∠E
∴△BDC∽△ECA
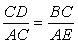
即AC·BC=AE·CD
.证明，连结EC，∵AE是直径
∴∠ACE=∠D=Rt∠
∠B=∠E
∴△BDC∽△ECA
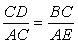
即AC·BC=AE·CD
∴∠ACE=∠D=Rt∠
∠B=∠E
∴△BDC∽△ECA
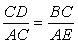
即AC·BC=AE·CD
练习册系列答案
阅读快车系列答案
相关题目
cm，
，∠ACB=30°.
