题目内容
如图，AB是⊙O的直径，C为⊙O上一点，AB和过C点的切线互相垂直，垂足为D，求证：AC平分∠DAB.
证明略
连结OC
∵CD是⊙O的切线，OC是半径
∴OC⊥CD
又∵AD⊥CD
∴AD∥OC
∴∠OCA=∠CAD
∵OC=OA
∴∠OAC=∠OCA
∴∠CAD=∠OAC
∴AC平分∠DAB
∵CD是⊙O的切线，OC是半径
∴OC⊥CD
又∵AD⊥CD
∴AD∥OC
∴∠OCA=∠CAD
∵OC=OA
∴∠OAC=∠OCA
∴∠CAD=∠OAC
∴AC平分∠DAB
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
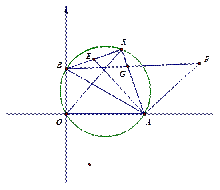
与坐标轴交于A（1，0）、B（5，0）两点，⊙
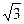，O）、(0，2)，P是△AOB外接圆上的一点，且∠AOP=45°，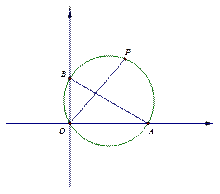
；
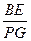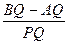
的直径，弦CD⊥AB于点E，且CD=3cm，⊙O的半径为
cm，则∠CDB的度数为（ ）
