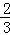题目内容
如图,在梯形ABCD中,AD∥BC,AC=AB,AC平分∠DAB,F为BC上一点,且BF=AD,连接DF交AC于E点,连接BE.
(1)求证:BE=DC;
(2)若AD=4,BC=6,求BE的长.

(1)求证:BE=DC;
(2)若AD=4,BC=6,求BE的长.

(1)见解析 (2)2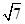
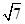
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠BAC.
∵AD∥BC,∠DAC=∠ACB
∴∠BAC=∠ACB,
∴AB=BC,
∵AC=AB,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠DAC=∠ACB=∠ACB=60°,
∵AD∥BC,AD=BF,
∴四边形ABFD是平行四边形,
∴DF∥AB,
∴∠CEF=∠AED=60°,
∴△CEF、△ADE都是等边三角形,
∴∠BFE=∠CED,EF=EC,DE=AD=BF,
∴△BFE≌△DEC,
∴BE=DC
(2)解:∵四边形ABFD是平行四边形,
∴DF=AB,BF=DE=AD
∵△ABC是等边三角形,
∴BC=AB=DF=6
作EG⊥BC于点G,
则由勾股定理得:EG=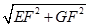 =
=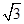 ,
,
∴在Rt△BEG中,
BE=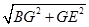 =
=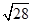 =2
=2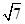 .
.
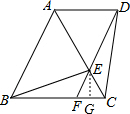
(1)分别证明△ABC、△CEF、△ADE都是等边三角形,然后证得△BFE≌△DEC,从而证得BE=DC;
(2)利用上题证得的平行四边形和等边三角形利用勾股定理求解即可.
∴∠DAC=∠BAC.
∵AD∥BC,∠DAC=∠ACB
∴∠BAC=∠ACB,
∴AB=BC,
∵AC=AB,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠DAC=∠ACB=∠ACB=60°,
∵AD∥BC,AD=BF,
∴四边形ABFD是平行四边形,
∴DF∥AB,
∴∠CEF=∠AED=60°,
∴△CEF、△ADE都是等边三角形,
∴∠BFE=∠CED,EF=EC,DE=AD=BF,
∴△BFE≌△DEC,
∴BE=DC
(2)解:∵四边形ABFD是平行四边形,
∴DF=AB,BF=DE=AD
∵△ABC是等边三角形,
∴BC=AB=DF=6
作EG⊥BC于点G,
则由勾股定理得:EG=
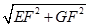 =
=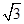 ,
,∴在Rt△BEG中,
BE=
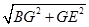 =
=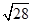 =2
=2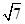 .
.
(1)分别证明△ABC、△CEF、△ADE都是等边三角形,然后证得△BFE≌△DEC,从而证得BE=DC;
(2)利用上题证得的平行四边形和等边三角形利用勾股定理求解即可.

练习册系列答案
相关题目




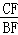 的值为( )
的值为( )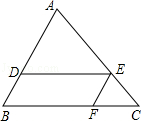
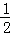 B.
B.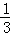 C.
C.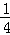 D.
D.