题目内容
【题目】如图1,点A是x轴正半轴上的动点,点B的坐标为(0,4),M是线段AB的中点.将点M绕点A顺时针方向旋转900得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点.连结AC,BC,CD,设点A的横坐标为t,
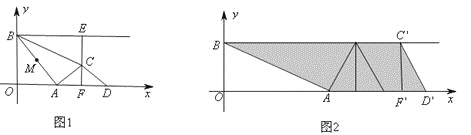
(1)当t=2时,求CF的长;
(2)①当t为何值时,点C落在线段CD上;
②设△BCE的面积为S,求S与t之间的函数关系式;
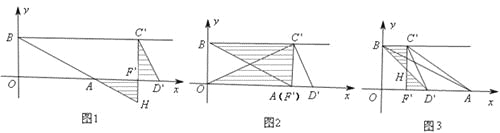
(3)如图2,当点C与点E重合时,将△CDF沿x轴左右平移得到![]() ,再将A,B,
,再将A,B,![]() 为顶点的四边形沿
为顶点的四边形沿![]() 剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出符合上述条件的点
剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出符合上述条件的点![]() 坐标,
坐标,
【答案】(1)CF=1;(2)①![]() ;②
;②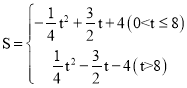 ;(3)点
;(3)点![]() 的坐标为:(12,4),(8,4),(2,4).
的坐标为:(12,4),(8,4),(2,4).
【解析】
(1)由Rt△ABO∽Rt△CAF即可求得CF的长.
(2)①点C落在线段CD上,可得Rt△CDD∽Rt△BOD,从而可求t的值.
②由于当点C与点E重合时,CE=4,![]() ,因此,分
,因此,分![]() 和
和![]() 两种情况讨论.
两种情况讨论.
(3)分三种情况作出图形讨论即可得到答案.
解:(1)当t=2时,OA=2,
∵点B(0,4),
∴OB=4.
又∵∠BAC=900,AB=2AC,
∴Rt△ABO∽Rt△CAF.
∴![]() ,
,
CF=1.
(2)①当OA=t时,
∵Rt△ABO∽Rt△CAF,
∴![]() .
.
∴![]() .
.
∵点C落在线段CD上,
∴Rt△CDD∽Rt△BOD.
∴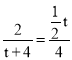 ,
,
整理得![]() .
.
解得![]() (舍去).
(舍去).
∴当![]() 时,点C落在线段CD上.
时,点C落在线段CD上.
②当点C与点E重合时,CE=4,可得![]() .
.
∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
综上所述,S与t之间的函数关系式为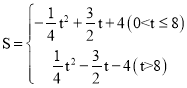 .
.
(3)(3)点![]() 的坐标为:(12,4),(8,4),(2,4).理由如下:
的坐标为:(12,4),(8,4),(2,4).理由如下:
如图1,当![]() 时,点
时,点![]() 的坐标为(12,0),
的坐标为(12,0),
根据![]() ,
,![]() 为拼成的三角形,此时点
为拼成的三角形,此时点![]() 的坐标为(12,,4).
的坐标为(12,,4).
如图2,当点![]() 与点A重合时,点
与点A重合时,点![]() 的坐标为(8,0),
的坐标为(8,0),
根据![]() ,
,![]() 为拼成的三角形,此时点
为拼成的三角形,此时点![]() 的坐标为(8,,4).
的坐标为(8,,4).
如图3,当![]() 时,点
时,点![]() 的坐标为(2,0),
的坐标为(2,0),
根据![]() ,
,![]() 为拼成的三角形,此时点
为拼成的三角形,此时点![]() 的坐标为(2,,4).
的坐标为(2,,4).
∴点![]() 的坐标为:(12,4),(8,4),(2,4).
的坐标为:(12,4),(8,4),(2,4).