Question

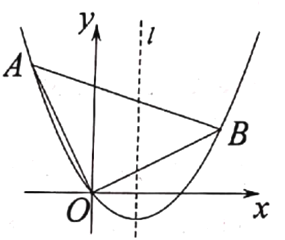
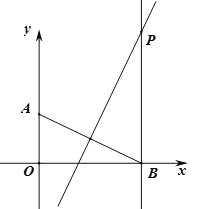
【题目】如图，在平面直角坐标系中，y轴上一点A（0,2），在x轴上有一动点B，连结AB，过B点作直线l⊥x轴，交AB的垂直平分线于点P(x,y)，在B点运动过程中，P点的运动轨迹是________,y关于x的函数解析式是________.

Answer 1

【答案】抛物线 y=x2+1

【解析】

当点B在x轴的正半轴上时，如图1，连接PA，作AC⊥PB于点C，则四边形AOBC是矩形，由P在AB的垂直平分线上可得PA=PB，进而可用y的代数式表示出PC、AP，在Rt△APC中根据勾股定理即可得出y与x的关系式；当点B在x轴的负半轴上时，用同样的方法求解即可.

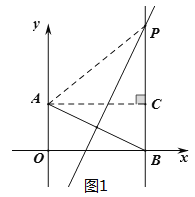
解：当点B在x轴的正半轴上时，如图1，连接PA，作AC⊥PB于点C，则四边形AOBC是矩形，

∴AC=OB=x，BC=OA=2，

∵P在AB的垂直平分线上，∴PA=PB=y，

在Rt△APC中，AC2+PC2=AP2，∴x2+(y2)2=y2，整理得y=x2+1；

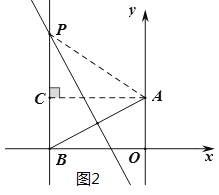
当点B在x轴的负半轴上时，如图2，同理可得y ，x满足的关系式是：y=x2+1，

∴y ，x满足的关系式是：y=x2+1.

故答案为：抛物线、y=x2+1.