题目内容
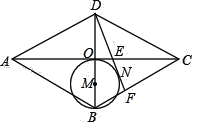
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则菱形ABCD的面积是( )
A. 24B. 20C. ![]() D.
D. ![]()
【答案】D
【解析】
连接MN,根据题意可得OE=1,因为DN为⊙M的切线,所以EN=EO=1,易证△DEO∽△DMN,且MN=![]() DM,则DE=3OE=3,在Rt△DMN中,利用勾股定理即可求得MN的长,即可得BD的长,再利用菱形的面积公式求解即可.
DM,则DE=3OE=3,在Rt△DMN中,利用勾股定理即可求得MN的长,即可得BD的长,再利用菱形的面积公式求解即可.
解:如图,连接MN,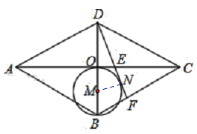
∵AE=5,CE=3,DN为⊙M的切线,
∴OE=EN=1,
易证△DEO∽△DMN,且MN=![]() DM,
DM,
则DE=3OE=3,
在Rt△DMN中,MN2+DN2=DM2,即MN2+16=9 MN2,
解得MN=![]() ,则BD=4MN=4
,则BD=4MN=4![]() ,
,
则菱形ABCD的面积=![]() BD·AC=
BD·AC=![]() .
.
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目