题目内容
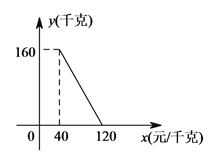
【题目】某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)根据图象,求y与x的函数关系式;
(2)商店想在销售成本不超过3000元的情况下,使销售利润达到2400元,问销售单价应定为多少元?
【答案】(1)y=-2x+240(40≤x≤120)(2) 销售单价应定为100元
【解析】
(1)设出函数解析式y=kx+b,把点(40,160),(120,0)代入,即可求出函数解析式.
(2)根据成本不超过3000元,进价×销售量≤3000,列不等式40(-2x+240)≤3000,解不等式求出x≥82.5,结合图形得出xd的取值范围82.5≤x≤120.再根据每千克的利润×销售量列出一元二次方程(x-40)(-2x+240)=2400,解方程得出![]() ,根据x的取值范围,得出销售价应为100元.
,根据x的取值范围,得出销售价应为100元.
(1)设y与x函数关系式y=kx+b,把点(40,160),(120,0)代入得
![]() 解得
解得![]()
∴y与x函数关系式为y=-2x+240(40≤x≤120).
(2)由题意,销售成本不超过3000元,得
40(-2x+240)≤3000.
解不等式得x≥82.5,
∴82.5≤x≤120.
根据题意列方程,得(x-40)(-2x+240)=2400.
即x2-160x+6000=0,
解得x1=60,x2=100.
∵60<82.5,故舍去.
∴销售单价应该定为100元.

练习册系列答案
相关题目