题目内容
【题目】问题提出
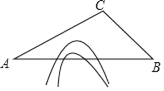
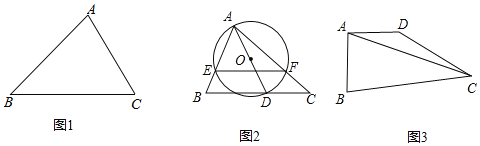
（1）如图1，在△ABC中，∠A＝75°，∠C＝60°，AC＝6
，求△ABC的外接圆半径R的值；
问题探究
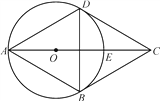
（2）如图2，在△ABC中，∠BAC＝60°，∠C＝45°，AC＝8
，点D为边BC上的动点，连接AD以AD为直径作⊙O交边AB、AC分别于点E、F，接E、F，求EF的最小值；
问题解决
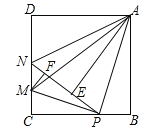
（3）如图3，在四边形ABCD中，∠BAD＝90°，∠BCD＝30°，AB＝AD，BC+CD＝12
，连接AC，线段AC的长是否存在最小值，若存在，求最小值：若不存在，请说明理由．
【答案】（1）△ABC的外接圆的R为6；（2）EF的最小值为12；（3）存在，AC的最小值为9
．
【解析】
（1）如图1中，作△ABC的外接圆，连接OA，OC．证明∠AOC=90°即可解决问题；
（2）如图2中，作AH⊥BC于H．当直径AD的值一定时，EF的值也确定，根据垂线段最短可知当AD与AH重合时，AD的值最短，此时EF的值也最短；
（3）如图3中，将△ADC绕点A顺时针旋转90°得到△ABE，连接EC，作EH⊥CB交CB的延长线于H，设BE=CD=x．证明EC=
AC，构建二次函数求出EC的最小值即可解决问题．
解：（1）如图1中，作△ABC的外接圆，连接OA，OC．
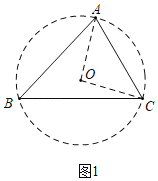
∵∠B＝180°﹣∠BAC﹣∠ACB＝180°﹣75°﹣60°＝45°，
又∵∠AOC＝2∠B，
∴∠AOC＝90°，
∴AC＝6，
∴OA＝OC＝6，
∴△ABC的外接圆的R为6．
（2）如图2中，作AH⊥BC于H．
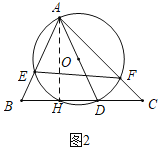
∵AC＝8
，∠C＝45°，
∴AH＝ACsin45°＝8×
＝8
，
∵∠BAC＝60°，
∴当直径AD的值一定时，EF的值也确定，
根据垂线段最短可知当AD与AH重合时，AD的值最短，此时EF的值也最短，
如图2﹣1中，当AD⊥BC时，作OH⊥EF于H，连接OE，OF．
∵∠EOF＝2∠BAC＝120°，OE＝OF，OH⊥EF，
∴EH＝HF，∠OEF＝∠OFE＝30°，
∴EH＝OFcos30°＝4
＝6，
∴EF＝2EH＝12，
∴EF的最小值为12．
（3）如图3中，将△ADC绕点A顺时针旋转90°得到△ABE，连接EC，作EH⊥CB交CB的延长线于Hspan>，设BE＝CD＝x．
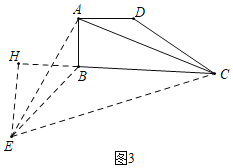
∵∠AE＝AC，∠CAE＝90°，
∴EC＝AC，∠AEC＝∠ACE＝45°，
∴EC的值最小时，AC的值最小，
∵∠BCD＝∠ACB+∠ACD＝∠ACB+∠AEB＝30°，
∴∠∠BEC+∠BCE＝60°，
∴∠EBC＝120°，
∴∠EBH＝60°，
∴∠BEH＝30°，
∴BH＝
x，EH＝x，
∵CD+BC＝12，CD＝x，
∴BC＝12﹣x
∴EC2＝EH2+CH2＝（x）2+
＝x2﹣12x+432，
∵a＝1＞0，
∴当x＝﹣
＝6时，EC的长最小，
此时EC＝18，
∴AC＝EC＝9，
∴AC的最小值为9．
