Question

【题目】如图，在平面直角坐标系中，抛物线和抛物线相交于点、（点在点的左侧），是抛物线上段的一点（点不与、重合），过点作轴的垂线交抛物线于点，以为边向右侧作正方形．设点的横坐标为，当正方形的四个顶点分别落在四个不同象限时，的取值范围是__________．

Answer 1

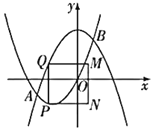
【答案】

【解析】

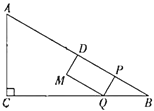
若正方形的四个顶点分别落在四个不同象限，则P点在第三象限，Q点在第二象限，M点在第一象限，N点在第四象限，由点的横坐标为， 通过解析式可表示点P、Q的坐标，即可表示PQ的长，通过正方形的边长相等可表示N点的横坐标，通过象限内点的坐标特点求解即可．

解：若正方形的四个顶点分别落在四个不同象限，则P点在第三象限，Q点在第二象限，M点在第一象限，N点在第四象限，

∵点的横坐标为，是抛物线上段的一点

∴，，

由题意可知Q点和P点横坐标相同，

∴，

若Q在Q点在第二象限，则，

解得，或（舍），

∴，即，

∴M、N的横坐标都为，

∵M点在第一象限，N点在第四象限，

∴，

当时，解得，，

因此时，

又∵，

∴，

故答案为：．