题目内容
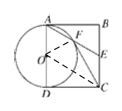
【题目】如图,四边形ABCD为矩形,E为BC边的中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.求证:CF与⊙O相切.

【答案】证明见解析
【解析】整体分析:
连接OF,OC,先证四边形OAEC是平行四边形,用SAS证明△ODC≌△OFC,得到∠OFC=∠ODC=90°即可.
证明:连接OF,OC.
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ADC=90°.
∵E为BC边的中点,AO=DO,
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形,∴AE∥OC,∴∠DOC=∠OAF,∠FOC=∠OFA.
∵OA=OF,∴∠OAF=∠OFA,∴∠DOC=∠FOC.
∵在△ODC和△OFC中,
OD=OF,∠DOC=∠FOC,OC=OC,
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与⊙O相切.

练习册系列答案
相关题目