题目内容
【题目】如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连结AF、BD.
(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;
(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.

【答案】(1)猜想:AF=BD且AF⊥BD.
证明:设AF与DC交点为G.
∵FC=DC,AC=BC,∠BCD=∠BCA+∠ACD,
∠ACF=∠DCF+∠ACD,∠BCA=∠DCF=90°,
∴∠BCD=∠ACF.
∴△ACF≌△BCD.
∴AF=BD.,∠AFC=∠BDC.
∵∠AFC+∠FGC="90°," ∠FGC=DGA,
∴∠BDC+∠DGA=90°.
∴AF⊥BD.
∴AF=BD且AF⊥BD.
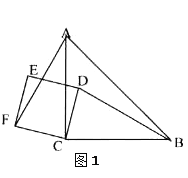
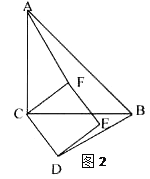
(2)如图,结论:AF=BD且AF⊥BD.
图形不惟一,只要符合要求即可.
如:图1中CD边在△ABC的内部;图2中CF边在△ABC的内部.
【解析】一般线段的关系有数量关系和位置关系,此题AF与DB的关系是AF=BD且AF⊥BD,要证明它们可以利用等腰直角三角形性质和正方形的性质构造全等条件证明△ACF≌△BCD,然后利用全等三角形的性质可以解决题目的问题.

练习册系列答案
相关题目