题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=30cm,BC=40cm.点P从点A出发,以5cm/s的速度沿AC向终点C匀速移动.过点P作PQ⊥AB,垂足为点Q,以PQ为边作正方形PQMN,点M在AB边上,连接CN.设点P移动的时间为t(s).

(1)PQ=______;(用含t的代数式表示)
(2)当点N分别满足下列条件时,求出相应的t的值;①点C,N,M在同一条直线上;②点N落在BC边上;
(3)当△PCN为等腰三角形时,求t的值.
【答案】(1)4t;(2)①![]() ,②
,②![]() ;(3)
;(3)![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)先求出AB=50,sinA=![]() =
=![]() ,cosA=
,cosA=![]() =
=![]() ,进而求出AQ=3t,PQ=4t,即可得出结论;
,进而求出AQ=3t,PQ=4t,即可得出结论;
(2)先判断出PN=QM=PQ=4t,
①求出CD=24,AD=18,进而判断出AQ+QM=AD=18,建立方程即可得出结论;
②判断出∠APQ=∠PNC,进而得出△AQP∽△PCN,建立方程即可得出结论;
(3)分三种情况,利用等腰三角形的性质建立方程求解即可得出结论.
解:(1)在Rt△ABC中,根据勾股定理得,AB=50,
∴sinA=![]() =
=![]() ,cosA=
,cosA=![]() =
=![]()
∵PQ⊥AB,
∴∠AQP=90°,
由运动知,AP=5t,
在Rt△AQP中,AQ=APcosA=![]() ×5=3t,PQ=APsinA=4t,
×5=3t,PQ=APsinA=4t,
故答案为:4t;
(2)由(1)知,AQ=3t,PQ=4t,
∵四边形PQMN是正方形,
∴PN=QM=PQ=4t,
①如图1,
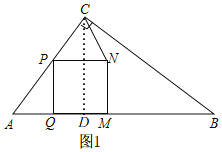
由(1)知,AB=50,
过点C作CD⊥AB于D,
∴![]() ABCD=
ABCD=![]() ACBC,
ACBC,
∴CD=24,
在Rt△ADQ中,AD=![]() =18,
=18,
∵点C,N,M在同一条直线上,
∴点M落在点D,
∴AQ+QM=AD=18,
由(1)知,QM=PQ=4t,AQ=3t,
∴4t+3t=18,
∴t=![]() ;
;
②点N落在BC上时,∠PCN=∠PCB=90°=∠AQP,
∴∠CPN+∠CNP=90°,
∵∠QPN=90°
∴∠CPN+∠APQ=90°,
∴∠APQ=∠PNC,
∵∠AQP=∠PCN,
∴△AQP∽△PCN,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ;
;
(3)当PC=PN时,30-5t=4t,
∴t=![]() ,
,
当PC=NC时,如图2,过点C作CF⊥PN于F,延长CF交AB于D,
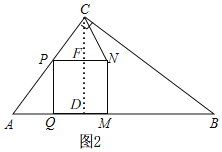
∴PF=![]() PN=2t,
PN=2t,
∴QD=2t,
根据勾股定理得,AQ=![]() =3t,
=3t,
∴AD=AQ+QD=5t=18,
∴t=![]() ,
,
当PN=NC时,如图3,过点N作NG⊥AC于G,
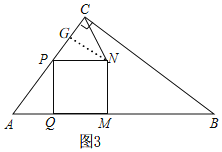
∴PG=![]() PC=
PC=![]() ,
,
易知,△PNG∽△APQ,
∴![]() ,
,
∴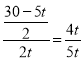 ,
,
∴t=![]() ,
,
即:当△PCN是等腰三角形时,![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.