题目内容
【题目】在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)写出点C的坐标;
(2)求证:MD=MN;
(3)连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明

【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)见解析;(3)MN平分∠FMB成立,证明见解析
;(2)见解析;(3)MN平分∠FMB成立,证明见解析
【解析】
(1)根据四边形OBCD是正方形所以点C的坐标应该是C(2,2);
(2)可通过构建全等三角形来求解.在OD上取OH=OM,通过证三角形DHM和MBN全等来得出DM=MN.
(3)本题也是通过构建全等三角形来求解的.在BO延长线上取OA=CF,通过三角形OAD,FDC和三角形DAM,DMF这两对全等三角形来得出FM和OM,CF的关系,从而得出FM是否是定值.然后再看∠FMN是否与∠NME相等.
(1)∵四边形![]() 是正方形,
是正方形,![]() ,
,
∴![]()
∴点![]() 的坐标为
的坐标为![]()
(2)在OD上取OH=OM,连接HM,
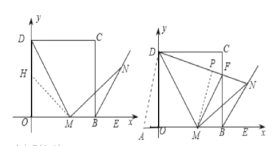
∵OD=OB,OH=OM,
∴HD=MB,∠OHM=∠OMH,
∴∠DHM=180°45°=135°,
∵NB平分∠CBE,
∴∠NBE=45°,
∴∠NBM=180°45°=135°,
∴∠DHM=∠NBM,
∵∠DMN=90°,
∴∠DMO+∠NMB=90°,
∵∠HDM+∠DMO=90°,
∴∠HDM=∠NMB,
在△DHM和△MBN中,
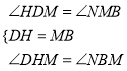 ,
,
∴△DHM≌△MBN(ASA),
∴DM=MN.
(3)MN平分∠FMB成立。证明如下:
在BO延长线上取OA=CF,可证△DOA≌△DCF,△DMA≌△DMF,
FM=MA=OM+CF(不为定值),∠DFM=∠DAM=∠DFC,
过M作MP⊥DN于P,则∠FMP=∠CDF,
由(2)可知∠NMF+∠FMP=∠PMN=45°,
∠NMB=∠MDH,∠MDO+∠CDF=45°,
进一步得∠NMB=∠NMF,即MN平分∠FMB.

 阅读快车系列答案
阅读快车系列答案【题目】某校召开运动会,七(1)班学生到超市分两次(第二次少于第一次)购买某种饮料90瓶,共用去205元,已知该种饮料价格如下:
购买瓶数/瓶 | 不超过30 | 30以上不超过50 | 50以上 |
单价/元 | 3 | 2.5 | 2 |
求:两次分别购买这种饮料多少瓶?
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?