题目内容
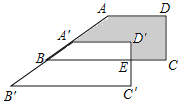
【题目】如图，在四边形ABCD中，AD∥BC，∠BCD＝90°，将四边形ABCD沿AB方向平移得到四边形A'B'C'D'，BC与C'D'相交于点E，若BC＝8，CE＝3，C'E＝2，则阴影部分的面积为（ ）
A.12+2
B.13C.2
+6D.26
【答案】B
【解析】
利用平移的性质得到B′C′＝BC＝8，BC∥B′C′，CD∥C′D′，S梯形ABCD＝S梯形A′B′C′D′，然后根据S阴影部分＝S梯形BB′C′E进行计算．
解：∵四边形ABCD沿AB方向平移得到四边形A'B'C'D'，
∴B′C′＝BC＝8，BC∥B′C′，CD∥C′D′，S梯形ABCD＝S梯形A′B′C′D′，
∴C′D′⊥BE，
∴S阴影部分＝S梯形BB′C′E＝
（8﹣3+8）×2＝13．
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
